<<
Back to Kanarev's Physchemistry Book Index
5. PHOTON MODEL SEARCH
5.1. The direction of the search
The photon remains today the most mysterious creation of Nature. The
attempts of the scientists to discover its electromagnetic structure by means
of analysis of boundless experimental information concerning behavior of photon with the help of existing physical
theories till present time have not given a positive result [138], [155],
[156], [160]. The main reason of such state is in the fact that in reality the
photon behaves within the frames of space-matter-time unity axiom, and the
physicists try to analyze its behavior with the help of theories which operate outside this axiom
[153].
In order to find out electromagnetic model of proton it is necessary to
find such theories and such mathematical models which do not contradict
the above-mentioned axiom.
Mathematical relations which are used for the calculation of energies of
photons and electrons are the safest ones. As the results of these calculations
coincide with the results of experiments completely, we can have faith in such
formulas. They are usually called corpuscular mathematical relations, because
they describe corpuscular properties of photons. Due to the above-mentioned
facts, an experiment and the mathematical relations, which describe proton as a
corpuscle, remain the main source of information [158], [163], [164], [165].
Thus, energies of protons ![]() is calculated according to the formulas, respectively:
is calculated according to the formulas, respectively:
![]() (11)
(11)
![]() (12)
(12)
Here ![]() is the frequency of
oscillations of the photon,
is the frequency of
oscillations of the photon, ![]() is Planck’s constant,
is Planck’s constant,
![]() is mass of the
photon,
is mass of the
photon, ![]() is its speed.
is its speed.
It is considered that the electromagnetic structure of the photon has
wave nature, that’s why its speed in the wave length interval is determined
according to the formula
![]() (13)
(13)
Here ![]() is wave oscillation
frequency, i.e. number of its oscillations per second,
is wave oscillation
frequency, i.e. number of its oscillations per second, ![]() is wave length.
is wave length.
It
is clear from formulas (11), (12) and (13) that Planck’ constant has the
following appearance.
![]() (14)
(14)
We have got the mathematical expression of Planck’s constant ![]() . It has dimensionality, which is called moment in classical
mechanics and angular momentum in physics [44], [45]. We choose a designation
angular momentum, and we pay attention to the fact that it characterizes
rotation of any body. In this case in order to realize the space-matter-time
unity axiom it is enough that the symbols of space, matter and time are present
in the mathematical expression of angular momentum at the same time. Let us consider
mathematical expression of Planck’s constant (14). Here the mathematical symbol
. It has dimensionality, which is called moment in classical
mechanics and angular momentum in physics [44], [45]. We choose a designation
angular momentum, and we pay attention to the fact that it characterizes
rotation of any body. In this case in order to realize the space-matter-time
unity axiom it is enough that the symbols of space, matter and time are present
in the mathematical expression of angular momentum at the same time. Let us consider
mathematical expression of Planck’s constant (14). Here the mathematical symbol
![]() corresponds to
matter, the symbol
corresponds to
matter, the symbol ![]() corresponds to space,
and symbol v corresponds to time. It means that the space-matter-time
unity axiom is realized in Planck’s constant when it describes body rotation
process.
corresponds to space,
and symbol v corresponds to time. It means that the space-matter-time
unity axiom is realized in Planck’s constant when it describes body rotation
process.
The essence of angular momentum is clearly observed when a whipping top rotates. Angular momentum prevents
the whipping top from falling when it rotates. But the main thing is that
angular moment is vector quantity as well as speed, body motion acceleration or
force which influences it.
![]() Have a look at Fig.3, a. Speed
Have a look at Fig.3, a. Speed ![]() of point M
is vector quantity. It is directed tangentially to its trajectory. Vector
quantity
of point M
is vector quantity. It is directed tangentially to its trajectory. Vector
quantity ![]() , which coincides with the direction of vector
, which coincides with the direction of vector ![]() , is called quantity of motion of material particle or pulse
of particle.
, is called quantity of motion of material particle or pulse
of particle.
![]()
![]() Angular momentum
Angular momentum ![]() is vector quantity as
well. If the whipping top rotates counterclockwise (Fig.3, b), vector
is vector quantity as
well. If the whipping top rotates counterclockwise (Fig.3, b), vector ![]() is directed along
rotation axis upwards. This vector is
vector of angular momentum and prevents the whipping top from falling.
is directed along
rotation axis upwards. This vector is
vector of angular momentum and prevents the whipping top from falling.
If Planck’s constant has dimensionality of angular momentum and if
behaviour of elementary particles is described theoretically with its help,
these particles as a peg-top should rotate round their axes necessarily. For
many physics, it is an unexpected conclusion, and they cannot assume that
Planck’s constant has vector properties.
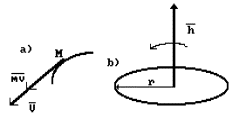
Fig. 3. Diagram to determination of notions:
motion quantity ![]() of material point, b) motion of momentum
of material point, b) motion of momentum
of the ring
or angular momentum of the ring ![]()
Actually Planck’s constant has
dimensionality of angular momentum, which has vector properties. But as
some physicists think, it does not mean that Planck’s constant is a vector
value [70]. We shall not contradict their stereotype mentality, let us use the
suitable possibility of hypothetical approach to this problem and
consider its fruitfulness.
On
this way we have to overcome a serious difficulty: we should find out what the
rotation radii of the photons and the electrons are equal to?
The matter is that in the
mathematical expression of Planck’s constant 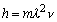 mass
mass 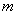 is multiplied
by square value of wave length
is multiplied
by square value of wave length 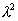 and
by frequency
and
by frequency 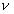 . But wave length characterizes wave process, and
dimensionality of Planck’s constant demonstrates that an electromagnetic
formation, which is described by it, rotates relative to the own axis, and we
are faced with the task to coordinate the wave process with the rotation one.
Detailed investigations carried out by us have shown that the photon and the
electron have such electromagnetic structures during rotation and motion, radii
. But wave length characterizes wave process, and
dimensionality of Planck’s constant demonstrates that an electromagnetic
formation, which is described by it, rotates relative to the own axis, and we
are faced with the task to coordinate the wave process with the rotation one.
Detailed investigations carried out by us have shown that the photon and the
electron have such electromagnetic structures during rotation and motion, radii
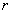 of which are equal to
lengths of their waves
of which are equal to
lengths of their waves 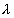 , i.e.
, i.e.
![]() (15)
(15)
Now Planck’s constant (14) has the following appearance
![]() . (16)
. (16)
It becomes clear that ![]() is moment of the
ring, and
is moment of the
ring, and ![]() is angular momentum
of the rotating ring. It points out to the fact that the photons and the
electrons have a form which is similar to the form of the rotating ring. As
Planck’s constant is vector value, the formula (11) for the determination of energy of photon should
be written in the following way
is angular momentum
of the rotating ring. It points out to the fact that the photons and the
electrons have a form which is similar to the form of the rotating ring. As
Planck’s constant is vector value, the formula (11) for the determination of energy of photon should
be written in the following way
![]() . (17)
. (17)
If the rotation of the photon and the electron round their
axes is taken into consideration, it is necessary to introduce angular
frequency ω of their rotation instead of instead of linear
frequency ![]() . Taking into consideration that
. Taking into consideration that
![]() (18)
(18)
we shall have [43]:
![]() (19)
(19)
As it is obvious, we have vector
product of two parallel vectors ![]() and
and ![]() . As mathematicians say, it is equal to zero vector, to which
it is possible to attribute any direction, including the ones, which coincide
with the directions of these
. As mathematicians say, it is equal to zero vector, to which
it is possible to attribute any direction, including the ones, which coincide
with the directions of these ![]() and
and ![]() vector [43].
vector [43].
In practice only scalar product of
these vectors have been used
![]() (20)
(20)
As vectors ![]() and
and ![]() are not only
parallel, but their directions coincide, an angle between them is equal to
zero, that’s why formulae (19) and (20) acquires its traditional appearance
are not only
parallel, but their directions coincide, an angle between them is equal to
zero, that’s why formulae (19) and (20) acquires its traditional appearance
![]() (21)
(21)
The entry (19) has only theoretical meaning, it has not
been used in practical calculations, that’s why vector properties of Planck’s
constant have not been paid attention to. Later on we shall see that these
properties play a decisive role when molecules are formed from the atoms and
the ions of chemical elements. That’s why vector properties of Planck’s
constant can serve as a foundation of the future theoretical chemistry.
But as my experience with the physicists has shown, this explanation is
insufficient for them. It inevitably causes a difficulty, which takes place in
the formation of energies of single photons and single
electrons. The first and the strongest objection is as follows: energy cannot
be vector value. It is true if one bears in mind the fact that heat energy is
totality of the photons. We live in this totality as a fish lives in water, no
vector proper ties of this totality have been registered. It is necessary to
dwell on this statement and to understand that vector properties are
characteristic to energies of not totality of photons and electrons, but to
single photons and electrons, which are disorderly oriented in this totality,
that’s why in general they do not give vector properties to it.
5.2. The photon is the Carrier of Energy and
Information
The photon is an electromagnetic formation being localized in space. Electromagnetic
radiation, which carries energy and information in space, originates from this
formation. As electromagnetic radiation transfers information and energy, the
photon is the elementary carrier of energy and information. It appears from
this that the structure of the photon is connected with the structure of
electromagnetic radiation, which is represented in the form a electromagnetic
wave (Fig.4) [125].
It is known that electromagnetic radiation is spread with velocity of
light ![]() . Its wavelength
. Its wavelength ![]() is changed in the
range of
is changed in the
range of ![]() and frequency
and frequency ![]() is changed in the
range of
is changed in the
range of ![]() . The whole electromagnetic spectrum is divided into bands
(Table 1).
. The whole electromagnetic spectrum is divided into bands
(Table 1).
Table 1. Electromagnetic spectrum bands
|
Bands |
Wave-length, m |
Oscillation frequency, s-1 |
|
1. Low-
frequency band |
|
|
|
2.
Broadcast band |
|
|
|
3.
Microwave band |
|
|
|
4. Relic
band (maximum) |
|
|
|
5.
Infrared band |
|
|
|
6. Light
band |
|
|
|
7.
Ultraviolet band |
|
|
|
8.
Roentgen band |
|
|
|
9. Gamma
band |
|
|
The wave-length of maximal intensity of
electromagnetic radiation of the whole Universe is nearly one millimetre (relic
band) [104], [105]. The law of the change of this intensity resembles the law
of intensity of radiation of a blackbody. That’s why it has been ascribed to
cooling of the Universe since the creation of the Universe [105].
One more hypothesis has appeared recently [8]. The relic radiation band
corresponds to the limit of existence of the single photons [26], [18]. There
are no single photons wit the wave-length of more than the wave-length of the
relic band. Maximum is formed here due to the fact that all photons with the
wave-length of less than the wave-length of relic radiation lose their energy
gradually in the process of their life interacting with the atoms and the
molecules of the environment in accordance with Compton effect, they increase
the wave length and enter the relic band [109].
Now
let’s recollect an idea of the Indian scientist Bose, who in 1924 supposed that
electromagnetic field is a collection of the photons, which has been called an
ideal photon gas by him [104]. Albert Einstein liked this idea very much, and
he translated his article from English into German and sent it to a journal of
physics [104]. Figure 4 shows Allan Holden’s concept concerning the formation
of electromagnetic wave-length by photon gas [106], [141].
The diagram is remarkable for the fact that according to Allan Holden,
an electromagnetic wave is formed by the pulses of single photons, which are
represented as the balls of different sizes by the author. The balls are the
photons. The question arises at once in what way does a size of the photon
depend on the length of the wave?
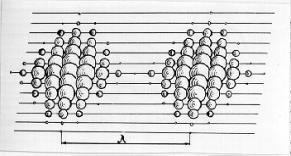
Fig. 4. Diagram of electromagnetic wave with
the length of l after Allan Holden [106]
Later on we’ll show that the wave-length ![]() of a single photon is
equal to radius
of a single photon is
equal to radius ![]() of its rotation, i.e.
the wave-length of the photon determines the area of location of each separate
photon in space [26], [18], [88]. In Fig. 4, radius of each ball is equal to
the wave-length of the photon, and the distance between the pulses of the
photons is equal to the wave-length, for example, of the radio signal.
of its rotation, i.e.
the wave-length of the photon determines the area of location of each separate
photon in space [26], [18], [88]. In Fig. 4, radius of each ball is equal to
the wave-length of the photon, and the distance between the pulses of the
photons is equal to the wave-length, for example, of the radio signal.
In relic range, the infrared photon has minimal energy ![]() , minimal
mass
, minimal
mass ![]() and minimal frequency
and minimal frequency
![]() , but maximal wave length
, but maximal wave length ![]() (or radius of
rotation
(or radius of
rotation ![]() ) (Table 1):
) (Table 1):
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
The gamma-photon has maximal energy ![]() maximal mass
maximal mass ![]() and maximal frequency
and maximal frequency ![]() , but minimal wave
length
, but minimal wave
length ![]() (or radius of
rotation
(or radius of
rotation ![]() ):
):
![]() (25)
(25)
![]() (26)
(26)
![]() (27)
(27)
As it is clear, the gamma photon is the least one, and the infrared
photon is the largest one.
Thus, maximal wave length of single photons corresponds to the relic
range, and the minimal wave length corresponds to gamma range (Table 1). From
the relic range to the gamma range, the wave length of the photon is reduced by
ten orders of magnitude, and frequency is increased in the same manner. As the photons
of all ranges move with one and the same velocity ![]() and form the
electromagnetic radiation waves, electromagnetic radiation velocity of all
ranges is one and the same [10], [109].
and form the
electromagnetic radiation waves, electromagnetic radiation velocity of all
ranges is one and the same [10], [109].
So, the suggested hypothesis divides the scale of electromagnetic
radiations into two classes: the photon one and the wave one. The photons are
single electromagnetic formations emitted by the electrons of the atoms. The
group of the photons emitted by the electrons of the atoms forms a field, which
is called an electromagnetic field. It can be continuous or pulsed (Fig. 4).
The pulses of the photons form the waves, which behaviour is studied in
electrodynamics. A detection of the structure of the photon is a task of
quantum mechanics.
The attempts to disclose the
structure of the photon with the help of Maxwell’s equations suggested by him
in 1865 are of no success [70], [106]. That’s why we’ll try to find another
approach to the solution of this task. We’ll begin from the detailed analysis
of the existing mathematical models, which describe behaviour of the photon
[109].
As a model of the photon remained unknown, the mathematical relations
describing its behaviour were not derived, but postulated. If the mathematical
relation describing behaviour of the photon at the complete lack of information
concerning its model were found, it would be a great achievement of theoretical
physics. These relations are as follows [4], [70], [109], [115], [116]:
relation of energy
![]() (28)
(28)
relation of
velocity
![]() (29)
(29)
relation of
pulse
![]() (30)
(30)
Planck’s constant
![]() (31)
(31)
Heisenberg’s inequality
![]() (32)
(32)
binding
between linear frequency ![]() and angular frequency
and angular frequency
![]()
![]() (33)
(33)
The equation of Louis de Broglie, which describes the wave properties of
the photon can be added to these relations.
![]() (34)
(34)
Thus, the electromagnetic model of the photon should be such that all
mathematical equations (28-34) describing its behaviour can be derived from the
analysis of its motion.
5.3. Photon Model Structure
As the photon has mass ![]() in motion, it is
natural that it has a centre of mass, i.e. such point, to which it is possible
to bring the whole mass of the photon, and motion of this point will
characterize motion of the whole photon. The wave properties of the photon
denote that this point (centre of mass) moves along wave track. Constant
velocity of motion of the photons of all ranges denotes that the tracks of
motion of the centres of masses of the photons of all frequencies are the same.
It is natural that in this case the structure of the photons of all frequencies
should be equal. Where is this structure hidden?
in motion, it is
natural that it has a centre of mass, i.e. such point, to which it is possible
to bring the whole mass of the photon, and motion of this point will
characterize motion of the whole photon. The wave properties of the photon
denote that this point (centre of mass) moves along wave track. Constant
velocity of motion of the photons of all ranges denotes that the tracks of
motion of the centres of masses of the photons of all frequencies are the same.
It is natural that in this case the structure of the photons of all frequencies
should be equal. Where is this structure hidden?
Let us pay attention to the fact that energies of the photons of all
frequencies are determined according to one and the same elementary formula ![]() . We write Planck’s constant in a spread form
. We write Planck’s constant in a spread form ![]() .
.
As Planck’s constant has dimensionality of angular momentum, its
persistence denotes that the law of conservation of angular momentum governs
this persistence.
We are overwhelmed by persistence of Planck’s constant [3], [11]. It is
confirmed by many calculations and many experimental data. It denotes that some
fundamental law of the nature governs persistence of Planck’s constant. Now we
see that this law is the law of conservation of angular momentum. It reads that
if no external force influences a rotating body, angular momentum of this body
remains constant [75], [98], [99].
What electromagnetic structure should the photon have in order to
provide this astonishing combination of its parameters (![]() ), which vary in such wide range that their product remains
constant? What forces should provide these changes and localization of the
photon in space during motion with such great velocity (
), which vary in such wide range that their product remains
constant? What forces should provide these changes and localization of the
photon in space during motion with such great velocity (![]() )? Let us consider
mathematical models, which determine energy of the photon:
)? Let us consider
mathematical models, which determine energy of the photon:
![]() . (35)
. (35)
As energies of the photons of all frequencies are equal to ![]() , mass m is the main changeable parameter of the photon. The photon has such electromagnetic
structure that the product of frequency of the photon
, mass m is the main changeable parameter of the photon. The photon has such electromagnetic
structure that the product of frequency of the photon ![]() by radius of its
rotation
by radius of its
rotation ![]() should remain
constant during the change of mass
should remain
constant during the change of mass ![]() .
.
As ![]() for the photons of
the whole scale of electromagnetic radiation, all of them should have such
structure that the change of mass
for the photons of
the whole scale of electromagnetic radiation, all of them should have such
structure that the change of mass ![]() would preserve the
product of frequency of the photon
would preserve the
product of frequency of the photon ![]() by radius of its
rotation
by radius of its
rotation ![]() constant and equal to
constant and equal to
![]() .
.
Thus, two constants hide the structure of the photon: Planck’s constant
and velocity of motion of the photon, i.e. velocity of light. According to
Planck’s constant, the structure of the photon should be such that the product
of mass of the photon ![]() by square of
wavelength
by square of
wavelength ![]() and by frequency v
will remain constant for the photon of any wavelength or vibration frequency.
Besides, the product of wavelength
and by frequency v
will remain constant for the photon of any wavelength or vibration frequency.
Besides, the product of wavelength ![]() by frequency v should
remain constant
by frequency v should
remain constant ![]() as well.
as well.
We have only one opportunity: we should suppose that persistence of
Planck’s constant ![]() and persistence of
velocity
and persistence of
velocity ![]() of motion of the
photons of all ranges are ensured by equality between electromagnetic forces
generated by electromagnetic fields of the photon and centrifugal forces of
inertia influencing the centres of masses of these fields.
of motion of the
photons of all ranges are ensured by equality between electromagnetic forces
generated by electromagnetic fields of the photon and centrifugal forces of
inertia influencing the centres of masses of these fields.
How do these forces manage to take place? Electromagnetic nature of the
photon predetermines availability of the electromagnetic forces, and availability
of rotating mass predetermines availability of the centrifugal forces of
inertia. It appears from this that localization of the photon in space is
provided by the electromagnetic forces and the centrifugal forces of inertia
equalizing each other. As the centrifugal forces of inertia have radial
directions from the centre of rotation, the magnetic component of the
electromagnetic forces should have radial direction, but to the centre of
rotation.
Thus, the electromagnetic model of the photon should consist of the
parts influenced simultaneously by the magnetic forces directed to the centre
and the centrifugal forces of inertia directed from the centre. It is natural
to suppose that these forces are applied at the distance of radius ![]() from the centre of
the model, i.e. in the points being the centres of separate electromagnetic
fields. We should accept that along the radii of the model such magnetic fields
are arranged, which are formed by the bar magnets.
from the centre of
the model, i.e. in the points being the centres of separate electromagnetic
fields. We should accept that along the radii of the model such magnetic fields
are arranged, which are formed by the bar magnets.
In order that the magnetic fields compress the model, the bar magnets of
two opposite radii should be directed to each other with unlike magnetic poles.
A question arises: how many magnetic poles should a model of the photon
contain? We’ll get an analytical answer to this question. Now we note that
radius ![]() of the models is
equal to the length of its wave
of the models is
equal to the length of its wave ![]() . Only under this condition, energy intensity of the motion
process of the photon model proves to be a minimal one [8], [18], [26].
. Only under this condition, energy intensity of the motion
process of the photon model proves to be a minimal one [8], [18], [26].
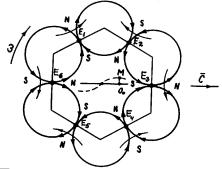
The diagram of electromagnetic model of the photon shown in Fig. 5, a
originates from this. The same model simulated by Walter Krauser, the German
physic [21], with the help of the constant magnets is given in Fig. 5, b.
As it is clear (Fig. 5), the model of
the photon consists of six magnetic fields, which are closed with each other,
are girded with electric fields during the motion of the model and pass into
electromagnetic fields. Magnetic fields of the photon are similar to magnetic
fields of the bar magnets. Field vectors of these magnetic fields alternate in
such a way that they are directed along one diameter in one and the same
direction at the opposite fields compressing the photon. As the photon is in
motion all the time, the magnetic forces compressing the photon are equalized
by the centrifugal forces.
The model is complicated, but only in this models the law of
conservation of angular momentum is realized in the following way.
It is known that if mass (energy) of the photon is increased, the length
of its wave is decreased. The model of the photon elicited by us shows why such legitimacy
exists. Because this process is governed by the law of conservation of angular
momentum ![]() . As mass m of the photon is increased, density of its
electromagnetic fields is increased (Fig. 5); due to this fact, the
electromagnetic forces compressing the photon are increased; all the time, they
are equalized by the centrifugal forces of inertia influencing the centres of
masses of these fields. It leads to the reduction of the photon rotation radius
. As mass m of the photon is increased, density of its
electromagnetic fields is increased (Fig. 5); due to this fact, the
electromagnetic forces compressing the photon are increased; all the time, they
are equalized by the centrifugal forces of inertia influencing the centres of
masses of these fields. It leads to the reduction of the photon rotation radius ![]() , which is always equal to the length of its wave
, which is always equal to the length of its wave ![]() . But as radius
. But as radius ![]() is squared in the
expression of Planck’s constant, photon vibration frequency
is squared in the
expression of Planck’s constant, photon vibration frequency ![]() should be increased
in order to preserve persistence of Planck’s constant. Due to it, an
insignificant change of mass of the photon changes its rotation radius
should be increased
in order to preserve persistence of Planck’s constant. Due to it, an
insignificant change of mass of the photon changes its rotation radius ![]() and frequency
and frequency ![]() automatically in such
a way that angular momentum (Planck’s constant) remains constant. Thus,
preserving their electromagnetic structure the photons of all frequencies
change mass, frequency and wavelength in such a way that
automatically in such
a way that angular momentum (Planck’s constant) remains constant. Thus,
preserving their electromagnetic structure the photons of all frequencies
change mass, frequency and wavelength in such a way that ![]() . It means that the law of conservation of angular
momentum governs the principle of this change.
. It means that the law of conservation of angular
momentum governs the principle of this change.
|
a) |
b) |
Fig. 5. Diagrams of electromagnetic models of
the photon: a) theoretical model, b) simulated model [21]
We
get the same clear and explicit answer to the next fundamental question: why do
the photons of all frequencies move in vacuum with the same velocity?
It is so, because the change of photon frequency v is a consequence of
the change of its mass, which in its turn changing density of electromagnetic
fields of the photon leads to the change of its rotation radius, which is
always equal to the wavelength. These changes take place in such a way that the
product of frequency ![]() by the wavelength
by the wavelength ![]() is always constant
for the photons of all frequencies and is equal to
is always constant
for the photons of all frequencies and is equal to ![]() (29). It is important
to pay attention to the fact that velocity of the centre of mass M of the
photon (Fig. 5) should be changed in the interval of the wavelength in such a
way that its average value remains constant and equal to
(29). It is important
to pay attention to the fact that velocity of the centre of mass M of the
photon (Fig. 5) should be changed in the interval of the wavelength in such a
way that its average value remains constant and equal to ![]() (Fig. 5).
(Fig. 5).
If our assertions are correct, we should deduct analytically all
relations (28)-(34), which describe its behaviour, from the analysis of motion
of the model of the photon being obtained. To this effect, we should retrace
the wave motion of the centre of mass M of the whole photon and the centres of
mass ![]() of its separate
electromagnetic fields.
of its separate
electromagnetic fields.
There is a diagram of displacement of the centre of mass M of the photon
and the centre of mass ![]() of one of its
electromagnetic field in the interval of the length
of one of its
electromagnetic field in the interval of the length ![]() of one wave in Fig. 6
[8], [18], [26].
of one wave in Fig. 6
[8], [18], [26].
Centroidal motion M of the photon is simulated by point M, which is
situated at the distance ![]() from the centre of
conditional circumference of radius
from the centre of
conditional circumference of radius ![]()
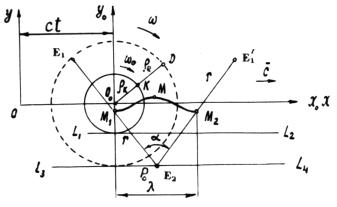
Fig. 6. Diagram of centroidal motion M of the
photon and the centre of mass E1 of one of its electromagnetic
field.
Centroidal motion ![]() of one
electromagnetic field of the photon is simulated by point
of one
electromagnetic field of the photon is simulated by point ![]() situated at a
distance of
situated at a
distance of ![]() from the centre of
mass M of the photon [8], [18], [26].
from the centre of
mass M of the photon [8], [18], [26].
The
Foundations of Physchemistry of Microworld
Copyright Ó2003 Kanarev Ph.
M.
Internet Version - http://book.physchemistry.innoplaza.net
<< Back to Physchemistry Book Index