<<
Back to Kanarev's Physchemistry Book Index
5.8. Analysis of Space Contortion and Black
Hole Formation
Newton’s law of gravitation (1687) encouraged the development of the
astronomical ideas [190], [114], [126]. First Michell (1783), then Laplace (1786)
predicted the possibility of existence of the stars with a strong enough
gravitational field that can retard the light photons, that’s why such stars
become invisible [91]. Later, they were called the black holes. Einstein’s
general theory of relativity predicts the existence of the black holes as well
[91].
In 1916, Karl Schwarzschild, the German astronomer and physicist, offers
a formula (89) for the calculation of the gravitational radius 
of the black hole,
which originates from the law of classical mechanics [91]. Since then this
formula has been used in the astronomic calculations, and the gravitational
radius is called Schwarzschild’s radius:
(89)
where 
is gravitational
constant, 
is mass of the star; 
is velocity of light.
It is known that as the photon wave length is reduced (from the infrared
to gamma range), its energy is increased by a factor of 
. The possibility of the photon to overcome the gravitational
force is increased in the same degree, but it is not taken into account in the
formula (89). We have every reason to believe that a mistake has been made when
the formula has been derived. What is its kernel? The formula (89) has been
derived in the following way. The mathematical relation of the law of
gravitation was been taken as a basis [109], [114]:
,
(90)
here: 
is gravitational
force; 
is the photon mass; 
is the distance
between the centres of the masses of the bodies, which form the gravitation.
In order to find the gravitational radius 
of a star, by which
its gravitational field retards light, it is necessary to find an equation
between the gravitational force 
and the force 
, which moves the photon. But it is not simple to do it when
there is no information concerning the electromagnetic structure of the photon.
That’s why the idea of the equality between the energy of the photon 
and the potential
energy of the gravitational filed 
. If we assume that
the gravitational force 
performs the work at
a distance, which is equal to the gravitational radius 
, this work will be
equal to [114]:
. (91)
The bond between the energy of the photon 
, its wave length 
, oscillation frequency 
and velocity 
is determined by the
dependencies [8], [18], [26]:
(92)
where 
is the Planck’s
constant; 
.
Then it has been assumed that the photon
will move in the gravitational field of the star with velocity 
, that’s why its kinetic energy should be determined by the
relation 
. When 
, we’ll have:
(93)
It means that the gravitational field of the star will retard the photon
when its potential energy (91) and kinetic energy of the photon (93) are equal,
i.e.:
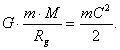(94)
We get the formula (89) for the calculation of the gravitational radius,
which has been suggested by K. Schwarzschild
(95)
The investigations carried out by us show that velocity of the centre of
mass of the photon is changed in the interval of its wave length in such a way
that its mean remain constant, and is equal to velocity of light. We can
determine the force 
, which moves the photon, in the first approximation by means
of division of its energy by the wave length [109], [114].
(96)
If we equate the gravitational force (90) and the force moving the
photon (96), we’ll have:
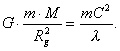(97)
It is clear that in order to convert the equation of the forces (97)
into the equation of energies (94) it is necessary to reduce the denominator of
the left-hand part by the gravitation radius 
and to reduce the
denominator of the right-hand side by the wave-length 
of the photon.
Actually it means that it is necessary
to equate the gravitation radius to the wave length of the photon. Certainly,
it is impossible to do it, but Schwarzschild did it, and his followers did not
notice this error. Thus, we have found the reason of the absence of the
wave-length of the photon in the formula (89) in order to calculate the
gravitational radius of the black hole. It is the result of Schwarzschild’s
mistake made by him when he has derived this formula.
It means that in order to determine the gravitational radius of the
black hole it is necessary to use the equality between the gravitational force
and the force, which moves the photon, but not the equality of energies.
Photon moving force (87) can be written in the following way
,
(98)
where 
is coefficient, which
value depends on acceleration used during calculation.
For maximal overall acceleration (86) 
; for maximal tangential acceleration (82) 
; for maximal value of projection of overall acceleration on
axis OX coinciding with the direction of centroidal motion of the photon 
. In our previous publications [180] we have assumed that 
. It corresponds to maximal overall acceleration of the point
of conventional circumference of radius 
. As the value of the above-mentioned coefficient exerts
insignificant influence on the value of acceleration of the centre of mass of
the photon, let us accept 
for the case being
considered by us.
If force (98) 
, which moves the photon, is equal to gravitational force
(90) 
, gravitational force of the gravitational field retards the
photon.
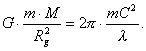(99)
We have the gravitational radius
(100)
Thus, we have got the formula for the calculation of the gravitational
radius of the black hole, which takes into consideration the wave-length of the
electromagnetic radiation.
Then the force 
, which moves the light photon with the wavelength 
with velocity 
, will be [130]:
(101)
Assuming that mass of the Sun is
, the radius of the Sun is 
, the gravitational constant 
and designating mass of the photon via
, we’ll
determine force 
of gravitation of the Sun, which influences the passing
photon, according to the formula [109],
[115]:
(102)
When the photon passes the Sun, tangent of the angle of deviation of the
photon from the straight-line motion will be equal to
.
If the photon the wavelength of 
passes the Sun along
the straight line, which is parallel to the line connecting the centres of
masses of the Sun and the Earth, the value of its deviation 
from the
straight-line motion in the vicinity of the Earth will be [101], [115]:
(103)
where 
is the distance from
the Earth to the Sun.
At present time, science has no
devices, which can register the value
.
Now
gravitational radius 
of the Sun, by which
it becomes a black hole, is determined according to the formula (89), which
does not take into account the wave-length of the photon [109], [115]:
(104)
Let us determine gravitational radii of the Sun for the infrared, light
and gamma photons with the following wave lengths, respectively: 
, 
и
(105)
(106)
(107)
Under the usual conditions, density r of the substance of the Sun is 
[89]. After compression, density of the substance of the Sun
will depend on the gravitational radius, which is determined according to the
formulas (104), (105), (106) and (107), respectively:
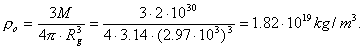(108)
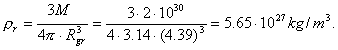(109)
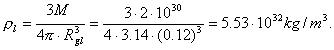(110)
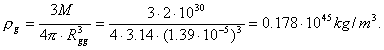(111)
Let us remind that density of nuclei of the atoms is determined by the
value 
[27].
It is clear that if the Sun is compressed to the gravitational radius 
(105), its
gravitational field will retard only the radiation of the far infrared range of
the spectrum. Electromagnetic radiation with smaller wave-length will penetrate
easily. In order to retard the photons of all frequencies, the gravitational
radius of the Sun should be 
(107); it is hardly
possible, because in this case density of the substance of the Sun should be
by 
greater than density
of nuclei of the atoms [109], [115].
Thus, an error in the determination of the gravitational radius of the
black hole according to the formula (89), which does not take into account the
wave length of the electromagnetic radiation, is 108, but the
astronomers do not know it yet [109], [115].
If the objects with such powerful gravitation, which retards
electromagnetic radiation, exist in the nature, not all of them can be black.
Their colours should be changed in compliance with the change of the colours of
the photons, which cannot be retarded by these objects. The photons from the
infrared range of the spectrum will be the first to be retarded; as the
gravitational radius is reduced, the photons of the light, ultraviolet,
roentgen and gamma ranges will be retarded. The hole becomes the black one only
in such a case when the gravitational radius corresponds to the gamma photon
with the minimal wave length.
5.9. Analysis of Michelson-Morley Experiment
The Russian scientist V.A. Atsyukovsky analysed rigorously the
experimental data of the basis of Einstein’s theories of relativity and came to
the following conclusion: “Analysis of the results of the experiments carried
out by various investigators in order to check the provision of STR and GTR
have proved that there are no experiments, in which positive and unambiguously
interpreted results have been obtained confirming provisions and conclusions of
theories of relativity of A. Einstein” [1].
This conclusion covers the most
famous experiment: Michelson-Morley experiment. Please, pay attention to the
fact that Michelson-Morley interferometer was stationary in relation to the
Earth; it was light that moved. The authors thought that they would be lucky
enough to register the influence of the Earth traverse speed 
in relation to the
Sun on light fringe deviation. The calculation was carried out according to the
formula [70]
(112)
Anticipated bias 0.04 of fringe was not registered. Somehow, the authors
did not try to find the reason of disaccords between the theory and the
experiment. Let us do it instead of them.
First of all, the photons have
mass. It means that their behaviour in the gravity force field should not
differ in this field from behaviour of other bodies, which have mass, for
example, from behaviour of a flying plane. Why did the idea fail to strike them
concerning the check the influence of the Earth rotation rate in relation to
the Sun on a plane’s flight? Both the plane and the photon have mass, that’s
why there should be no difference in
influence of their traverse speed in relation to the Sun in the field of the
Earth gravity force on their behaviour. Such influence on the plane is so small
that the devices fail to register it. The Earth rotation rate in relation to
its axis influences the plane’s flight. This rate should exert the same
influence on motion of light in the field of the Earth gravity force. In this
case, we should substitute not the Earth traverse speed in relation to the Sun
(
in the above-mentioned formula, but the Earth surface speed
(
) formed by its rotation in relation to its axis. Then the
anticipated bias of fringe in Michelson-Morley experiment will be not 0.04, but
significantly less: 0.00002. No wonder that Michelson-Morley device showed lack
of fringe bias. Now we know the reason: it has no indispensable sensitivity
(accuracy) [70].
What will happen if an experiment is carried out, in which a source of
light and a device registering the fringe bias move (rotate) in the Earth
gravitational field? In this case, the readings of the devices are compared
when there is no rotation of the whole installation and during its rotation. It
is clear that if there is no rotation of the installation, the principle of
measurements will not differ from the principle of measurements in
Michelson-Morley experiment, and the device will show no fringe bias. When the
installation begins its rotation in the Earth gravitational field, the bias of
the above-mentioned fringe should take place at once. It is explained by the
fact that when light travels from the source to the receiver, the latter’s position
is changed in the Earth gravitational field in relation to the source, and the
device should register bias of the above-mentioned fringe.
Let us emphasize once again: the position of the source and the signal
receiver in Michelson-Morley experiment
is not changed in relation to each other in the Earth gravitational field, and
it is changed in the example described by us. This is the main difference of
the above-mentioned experiments. The elementary logic being described is proved
by Sagnayk’s experiment. The results of his experiment contradict to the
readings of Michelson-Morley interferometer, and this fact is ignored by the
relativists. It proves the fact that they are not interested in scientific
truth [70].
We have given strong reasons of erroneousness of Einstein’s theories of
relativity. That’s why one is tempted to ask the question: how should we accept
the fact that his theories of relativity serve as a foundation of all
achievements of physics in this century as the relativists think? It is very
simple! All these achievements are the results of the efforts of the
physics-experimenters who have carried out the experiments in the order not to
check physical theories, but to get a result, which could be used for military
purposes or in competition on purpose to work up a sales market for their
products.
The theoreticians tried to find the explanation for these achievement
and to substantiate them somehow, but these explanations proved to be proximate
and superficial. The stereotype of thinking formed by erroneous Einstein’s
theories and inexplicable insistence of his adherents in protection of these
theories was a main retardation in
explanation of the deep principles of matter and creation.
History of science remembers no
case when the scientific ideas of any great scientist of the past, for example,
of I. Newton have been defended with the same fury as Einstein’s ideas of
relativity are defended. Albert Einstein was much more critical to his
scientific results than his adherents. Let us cite his opinion once more: “It
seems to them that I look at the results of my life with a halcyon
satisfaction. But everything is to the contrary if examined closely. There
exists no concept, in relation to which I am sure that it will remain
inviolable, and I am not convinced that I am on the right track.” (F. Hernek.
Albert Einstein. M., 1966, page 16).
These words do credit for their author. History of science knows many “irrefutable ideas”, which have proved to be erroneous during further development of science.
The
Foundations of Physchemistry of Microworld
Copyright Ó2003 Kanarev Ph.
M.
Internet Version - http://book.physchemistry.innoplaza.net
<< Back to Physchemistry Book Index