<<
Back to Kanarev's Physchemistry Book Index
7.
THE LAW OF THE RADIATION OF THE PERFECT BLACKBODY IS
THE LAW OF CLASSICAL
PHYSICS
7.1. General
Hitherto our search has been conducted within the framework of the laws
of classical physics. But it is known that at the end of the 19th century it
was announced that the law of classical physics operate successfully only in
the macro world, and in the microworld the different, quantum physical laws
operate. This point of view predominated during the whole 20th century. Now
when we have determined the models of the photon and the electron on the basis
of the laws of classical physics, a question arises: aren’t the physicists of
the former generations mistaken when they have burried the possibility of
classical physics to solve the problems of in the microworld? In order to give
a reply to this question, let us analyse attentively the sources of misbelief
to classical physics to solve the problems of
the microworld. Everything has begun from the deduction of the law of
radiation of the perfect blackbody.
The deduction of mathematical model
of the distribution law of the perfect blackbody made by Max Planck at the
beginning of the 20th century was based on notions and ideas, which are
considered to contradict the laws of classical physics [24], [102]. Planck
introduced constant h with dimensionality of mechanical action into the
mathematical model of distribution law of the perfect blackbody; it
contradicted to the electromagnetic nature of radiation. Nevertheless, his
mathematical model described experimental dependencies of this radiation. The
constant introduced by him pointed out to the fact that radiation takes place
not continuously, but in packets. It contradicted to Reyleigh - Jeans law,
which was based on classical notions concerning wave nature of electromagnetic
radiation, but described experimental dependencies in the low frequency range
only [24].
As the mathematical model of Reyleigh - Jeans law is present in the
mathematical model of the distribution law of the perfect blackbody, it means
that Planck distribution law of the perfect blackbody is based on the mutually
exclusive wave and corpuscular notions on nature of radiation [24], [102].
Continuous wave process of radiation with portal process was a safe
basis for acknowledgement of classical physics. Since that time the physics
began to think that the application field of the laws of classical physics is
restricted by the macro world. They think that other, quantum laws operate in
the micro world, that’s why physics, which
describes the microworld, should be called quantum physics. It should be noted
that Max Planck tried to understand the mixture of such physical notions and
return them to the classical way of development, but failed [24], [102], [108].
For the first time, the mathematical model of the law of the radiation of the
perfect blackbody connected with thermodynamic ideas was received by Yu.M.
Ageev [110], [112].
Years later, we have to admit that the border between the law of
classical physics and quantum physics has not been established yet. Still it is
difficult to solve many problems of the macro world, and many problems are
considered to be unsolved within the framework of the existing notions and conceptions,
that’s why we have to return to an attempt of Max Planck to derive a
mathematical model of the law of the perfect blackbody on the basis of
classical notions [70], [88].
7.2. Theoretical Part
First of all, let us give
Reyleigh - Jeans formula, which describes satisfactory experimental behaviour of a low frequency range of
radiation. Taking into consideration
the wave conceptions on electromagnetic radiation
they have found out that energy ![]() being available in
volume
being available in
volume ![]() of the perfect
blackbody is determined by the dependence [24]
of the perfect
blackbody is determined by the dependence [24]
![]() , (185)
, (185)
where ![]() is frequency of
radiation;
is frequency of
radiation;
![]() is volume of space of
the perfect blackbody;
is volume of space of
the perfect blackbody;
![]() is the speed of
light;
is the speed of
light;
![]() is Boltzmann
constant;
is Boltzmann
constant;
![]() is absolute radiation
temperature.
is absolute radiation
temperature.
If we divide the left part and the right part of the relation (185) by volume ![]() , we get volumetric
density
, we get volumetric
density ![]() of electromagnetic
radiation
of electromagnetic
radiation
![]() .
(186)
.
(186)
The deduction of this formula is based
the notion a number of standing
waves of electromagnetic radiation with frequency ![]() in the closed space
of the perfect blackbody [24].
in the closed space
of the perfect blackbody [24].
In order to get the mathematical model, which could describe the whole
range of electromagnetic radiation of the perfect blackbody, Max Planck
postulated that the radiation is not continuous but it is in packets, and energy ![]() of each radiated
packet is equal to
of each radiated
packet is equal to ![]() , and the formula for the calculation of density
, and the formula for the calculation of density ![]() of electromagnetic
radiation of the perfect blackbody is as follows (Fig. 19) [24]
of electromagnetic
radiation of the perfect blackbody is as follows (Fig. 19) [24]
![]() . (187)
. (187)

Fig. 19.
The experimental law of the radiation of black body
Value ![]() is a constant with
mechanical dimensionality of the action. The essence of this action was
completely unclear at that time. Nevertheless, the mathematical model obtained
by Planck gave a satisfactory description of the experimental laws of the radiation
of the perfect blackbody.
is a constant with
mechanical dimensionality of the action. The essence of this action was
completely unclear at that time. Nevertheless, the mathematical model obtained
by Planck gave a satisfactory description of the experimental laws of the radiation
of the perfect blackbody.
As it is clear, the expression ![]() in (187) significant addition to Reyleigh - Jeans formula (186),
in (187) significant addition to Reyleigh - Jeans formula (186), ![]() energy of one
radiated photon.
energy of one
radiated photon.
In order to understand the physical essence of Planck addition, one
should have a notion of electromagnetic
structure of the photon, because the physical essence of Planck constant ![]() is in this
structure. As the product
is in this
structure. As the product ![]() describes energies of
the photons the whole scale of
electromagnetic radiation,
electromagnetic structure of the photon is concealed in dimensionality of Planck constant.
describes energies of
the photons the whole scale of
electromagnetic radiation,
electromagnetic structure of the photon is concealed in dimensionality of Planck constant.
We have found out that the photon has
rotating electromagnetic structure, the centre
of mass describes the ![]() , which is equal to radius
, which is equal to radius ![]() of its rotation. As a result, of constant is as follows
(88)
of its rotation. As a result, of constant is as follows
(88)
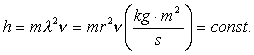 (88)
(88)
As it is clear, Planck constant has
clear mechanical dimensionality of angular momentum, which has another
name – moment of momentum. It is known [101] that the law of
conservation of angular momentum governs
constancy of angular momentum, and the reason clear. First of all, the
notion “the law of conservation of angular momentum” is notion
classical physics, to be more precise,
classical Newtonian mechanics. It means that
if no external force influences a rotating solid body, angular momentum of such body remains constant.
The photon is not a solid body but it has
mass ![]() , and we have every reason to believe photon an electromagnetic substance (i.e.
electromagnetic field) rotating in relation to the axis plays the role of mass. It results from the mathematical model (88)
of Planck constant that the electromagnetic model of the photon should be such
that simultaneous change of mass
, and we have every reason to believe photon an electromagnetic substance (i.e.
electromagnetic field) rotating in relation to the axis plays the role of mass. It results from the mathematical model (88)
of Planck constant that the electromagnetic model of the photon should be such
that simultaneous change of mass ![]() , radius
, radius ![]() and frequency
and frequency ![]() of the rotating
electromagnetic fields of the photon would retain their product reflected in the mathematical expression of
Planck constant (88) [109]. The diagram
of the rotating electromagnetic fields of the photon is in Fig. 5.
of the rotating
electromagnetic fields of the photon would retain their product reflected in the mathematical expression of
Planck constant (88) [109]. The diagram
of the rotating electromagnetic fields of the photon is in Fig. 5.
It is known that if mass
(energy) of photon is increased, its wavelength is decreased. This change is implemented
with the help of Planck constant (88) in the
model of the photon (Fig. 5) [109].
As the law of conservation of angular momentum (![]() ) governs constancy of constant, density of
their electromagnetic fields is increased when
the mass
) governs constancy of constant, density of
their electromagnetic fields is increased when
the mass ![]() of the photon (Fig.
5) is increased, and due to the
electromagnetic forces which are balanced by an equal
the centrifugal forces of inertia compressing the photon. This leads to the reduction of radius
of the photon (Fig.
5) is increased, and due to the
electromagnetic forces which are balanced by an equal
the centrifugal forces of inertia compressing the photon. This leads to the reduction of radius ![]() of photon rotation, which is always equal to
its wave length
of photon rotation, which is always equal to
its wave length ![]() . But as radius
. But as radius ![]() in the expression
of Planck constant is squared, oscillation frequency
in the expression
of Planck constant is squared, oscillation frequency ![]() should be increased in order to preserve constancy
of Planck constant (88). Due to this fact, a small alteration mass of the photon changes its rotation
radius and frequency automatically in such a way that angular momentum (Planck
constant) remains constant. Thus, the
photons of all frequencies preserving their electromagnetic structure change
mass, frequency and rotation radius in such a way that
should be increased in order to preserve constancy
of Planck constant (88). Due to this fact, a small alteration mass of the photon changes its rotation
radius and frequency automatically in such a way that angular momentum (Planck
constant) remains constant. Thus, the
photons of all frequencies preserving their electromagnetic structure change
mass, frequency and rotation radius in such a way that ![]() It means that the law of conservation of
angular momentum governs the principle of this alteration [101],
[109].
It means that the law of conservation of
angular momentum governs the principle of this alteration [101],
[109].
Why the photons of all frequencies move
in vacuum with equal speed? The answer is
alteration of frequency ![]() of the photon is a
consequence of the alteration of the
mass, which changes the
density of the electromagnetic fields of the photon and
the electromagnetic and centrifugal forces of inertia leads to the change radius of its rotation, which is always
equal to its wavelength. The above-mentioned changes take place in
such a way that the product of frequency
of the photon is a
consequence of the alteration of the
mass, which changes the
density of the electromagnetic fields of the photon and
the electromagnetic and centrifugal forces of inertia leads to the change radius of its rotation, which is always
equal to its wavelength. The above-mentioned changes take place in
such a way that the product of frequency ![]() and
and ![]() constant for the
photons of all frequencies and is equal to
constant for the
photons of all frequencies and is equal to ![]() . The speed of the centre of masses M of the photon (Fig. 5) is changed in such a way that its average value remains
constant and equal to
. The speed of the centre of masses M of the photon (Fig. 5) is changed in such a way that its average value remains
constant and equal to ![]() (Fig. 7) [109].
(Fig. 7) [109].
Thus, the law of conservation of
angular momentum, one of the fundamental laws of classical physics (to be more
precise, classical mechanics) governs
constancy of Planck constant ![]() . In modern
physics in classical mechanics it is
called the law of conservation of
moment of momentum [101]. It is
a purely classical mechanic law, not a mystical mechanical action as it has been
considered previously. That is why the appearance of constant in the mathematical model of the law of the radiation of the
perfect blackbody does not give the
reason to consider that classical physics is unable to describe the distribution
process of this body. On the contrary,
the law of conservation of angular momentum, the most fundamental law of
classical physics, takes part in the description of this process [70], [101],
[109]. Thus, Planck law of the
radiation of the perfect blackbody is a law of classical physics. The derivation of this law is based on classical notions given below.
. In modern
physics in classical mechanics it is
called the law of conservation of
moment of momentum [101]. It is
a purely classical mechanic law, not a mystical mechanical action as it has been
considered previously. That is why the appearance of constant in the mathematical model of the law of the radiation of the
perfect blackbody does not give the
reason to consider that classical physics is unable to describe the distribution
process of this body. On the contrary,
the law of conservation of angular momentum, the most fundamental law of
classical physics, takes part in the description of this process [70], [101],
[109]. Thus, Planck law of the
radiation of the perfect blackbody is a law of classical physics. The derivation of this law is based on classical notions given below.
7.3. Classical Derivation
of the Law of the Radiation of the
Perfect Blackbody
Use Reyleigh - Jeans ideas in
the calculation of a number of packets of electromagnetic radiation in the
space of the perfect blackbody,
describe a separate packet of electromagnetic radiation not as the
standing wave, but as the photon (Fig.
5) [4], [8], [18], [26], [109].
As radii of the closed electrical
fields of the photon are ![]() and radii of the centre mass of
electromagnetic fields are
and radii of the centre mass of
electromagnetic fields are ![]() the photon does not
have a spherical form, but a flat form
is nearly one fourth of the sphere with
radius
the photon does not
have a spherical form, but a flat form
is nearly one fourth of the sphere with
radius ![]() . Thus, the volume of
the localized space, in which the photon can be present, will be nearly
. Thus, the volume of
the localized space, in which the photon can be present, will be nearly ![]()
![]() . Volume
. Volume ![]() of the spherical space of radius
of the spherical space of radius ![]() of the perfect
blackbody will many orders of magnitude
greater than the volume of the photon. Maximal quantity
of the perfect
blackbody will many orders of magnitude
greater than the volume of the photon. Maximal quantity ![]() of the photons in
this space (as well as maximal quantity
of standing waves in Reyleigh - Jeans
formula) will be determined by a dependence
of the photons in
this space (as well as maximal quantity
of standing waves in Reyleigh - Jeans
formula) will be determined by a dependence
![]() . (188)
. (188)
Taking into consideration that ![]() , we’ll have
, we’ll have
![]() . (189)
. (189)
The interval of frequencies from ![]() to
to ![]() , the
number will be
, the
number will be
![]() .
(190)
.
(190)
As the photon moves linearly and
rotates round its axis in three-dimensional Euclidean space, it will have six
grades of freedom. Taking into consideration and dividing the left and
the right parts (190) by volume ![]() , volumetric
density
, volumetric
density ![]() of photons in the spherical space of the perfect blackbody as
shown below:
of photons in the spherical space of the perfect blackbody as
shown below:
![]() .
(191)
.
(191)
We integrate, we get
![]() (192)
(192)
Thus, we have volumetric density
(192) of the photons in the spherical space of the perfect blackbody. If
spherical space has a small hole, energy that
is emitted via this hole, will depend
energy of each photon ![]() , to be more precise, on its frequency
, to be more precise, on its frequency ![]() . Then the photons, which have passed via hole in the spherical space, will be
absorbed. As energy of each photon on the plane of its polarization is
realized by two grades of freedom, the value of heat energy of the absorbed
photons will be equal to
. Then the photons, which have passed via hole in the spherical space, will be
absorbed. As energy of each photon on the plane of its polarization is
realized by two grades of freedom, the value of heat energy of the absorbed
photons will be equal to ![]() . It means that volumetric density of the radiation
of the perfect blackbody will depend on energy
. It means that volumetric density of the radiation
of the perfect blackbody will depend on energy ![]() of each radiated
photon and energy
of each radiated
photon and energy ![]() of the whole set photons.
of the whole set photons.
As the radiation of the perfect
blackbody is a set of the photons, each of which has only kinetic energy, we
should introduce kinetic energy ![]() of the photon and
heat energy
of the photon and
heat energy ![]() of the set of the
radiated photons into the mathematical model of the distribution [24]
of the set of the
radiated photons into the mathematical model of the distribution [24]
![]() . (193)
. (193)
We should take into account that
the photons are emitted by the electrons of the atoms during their energy
transitions. Each electron can make a
series of transitions levels ![]() emitting the photons of various energy. The
complete distribution of volumetric density of energy emitted photons will consist of a sum of the distributions, which
take into account energies of the
photons of all energy levels. With due
regard for the above - mentioned facts, Maxwell law, which takes into
account energy distribution of the
photons all (
emitting the photons of various energy. The
complete distribution of volumetric density of energy emitted photons will consist of a sum of the distributions, which
take into account energies of the
photons of all energy levels. With due
regard for the above - mentioned facts, Maxwell law, which takes into
account energy distribution of the
photons all (![]() ) energy levels of the atom,
be put down in the following way
) energy levels of the atom,
be put down in the following way
![]() , (194)
, (194)
where ![]() is the main quantum
number determines of the position of
electron in the atom.
is the main quantum
number determines of the position of
electron in the atom.
It is known that sum of row (194)
is equal to [24]
![]() . (195)
. (195)
If we multiply the right part of volumetric density of the photons (192)
in the space of the perfect blackbody by a mathematical expression (195) of the
distribution law of this density and by energy of one photon ![]() , we get volumetric density
, we get volumetric density ![]() of energy which is radiated
by the perfect blackbody
of energy which is radiated
by the perfect blackbody
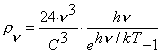 . (196)
. (196)
It is the law of the radiation of the perfect blackbody (187) as
obtained by Max Planck. Expression
(196) differs from expression (187)
coefficient ![]() . According to E.V.
Shpolsky [24], the value of this coefficient depends on the character of electromagnetic radiation and can vary from
. According to E.V.
Shpolsky [24], the value of this coefficient depends on the character of electromagnetic radiation and can vary from ![]() to
to ![]() . But within
the framework of the above-mentioned notions, the coefficient
. But within
the framework of the above-mentioned notions, the coefficient
![]() (197)
(197)
acquires a precise
physical sense. It characterizes (as it
should) density of the photons in the
cavity of the perfect blackbody.
The value ![]() does not change
the law of the
radiation of the perfect
blackbody, why more precise value of
this coefficient can be determined by experiment.
does not change
the law of the
radiation of the perfect
blackbody, why more precise value of
this coefficient can be determined by experiment.
Thus, we have derived the law of the radiation of the perfect blackbody on the
grounds of purely classical notions and ideas, and we see no reason to believe
that this law contradicts classical
physics. On the contrary, it follows from the laws of this physics. . All components of the mathematical
model of the law (196) of radiation of the perfect blackbody have got an
appropriate clear physical sense.
The
Foundations of Physchemistry of Microworld
Copyright Ó2003 Kanarev Ph.
M.
Internet Version - http://book.physchemistry.innoplaza.net
<< Back to Physchemistry Book Index