<<
Back to Kanarev's Physchemistry Book Index
8.8. Spectra of Valence Electrons of
Some Atoms of Chemical Elements
Carbon has six electrons. Its
electron having the smallest ionization energy ![]() =11.256 eV and the following row of excitation energies corresponding
to the stationary energy levels [5]: 7.48; 7.68; 7.95; 9.68; 9.71; 9.83;
10.38; 10.39; 10.40; 10.42; 10.43; 10.71; 10.72; 10.73; 10.88;
=11.256 eV and the following row of excitation energies corresponding
to the stationary energy levels [5]: 7.48; 7.68; 7.95; 9.68; 9.71; 9.83;
10.38; 10.39; 10.40; 10.42; 10.43; 10.71; 10.72; 10.73; 10.88;
10.89; 10.99; 13.12 eV is considered to be the
most active valency electron. The first three underlined values are so close
that we have every reason to suppose that they belong to the triplet, that’s
why let us find their average value (7.48+7.69+7.95)/3=7.70 eV. Then the
difference of energies will be equal to ![]() =11.26-7.70=3.56 eV, and fictitious binding energy with the
atomic nucleus corresponding to the first energy level will be as follows:
=11.26-7.70=3.56 eV, and fictitious binding energy with the
atomic nucleus corresponding to the first energy level will be as follows: ![]() =3.56× 4=14.24 eV. If we insert
=3.56× 4=14.24 eV. If we insert ![]() =11.256 eV and
=11.256 eV and ![]() =14.24 eV into the formulas (206) and (207), we’ll find
(Table 20).
=14.24 eV into the formulas (206) and (207), we’ll find
(Table 20).
Table 20. Spectrum of the first electron in the carbon
atom
|
Values |
n |
2 |
3 |
4 |
5 |
6 |
|
|
eV |
7.68 |
9.67 |
10.37 |
10.69 |
10.86 |
|
|
eV |
7.70 |
9.68 |
10.38 |
10.71 |
10.88 |
|
|
eV |
3.58 |
1.58 |
0.89 |
0.57 |
0.39 |
Let us prepare our reader to surprises,
which we can meet during the analysis of the structure of the nuclei and the
atoms of chemical elements. The first surprise is in the fact that binding
energy of all electrons with the atomic nuclei being in free state, which are
approximately the same. On the face of it, this conflicts with the experiment,
because it gives various values of binding energies of various electrons with
the atomic nuclei. But one should take into consideration the conditions of the
experiments, which have such differences.
The process of fixation of the
spectral lines takes place under the conditions of a transition of the atoms to
free state. Almost all the electrons of the atom have approximately the same
opportunity to separate from it. When one electron has left the atom, the
released proton in the nucleus begins to spread its influence on other
electrons increasing their attraction to the nucleus and, consequently, binding
energy.
Usually, the electrons from the atom
are removed consequently one by one. As each of them interacts with one proton
of the nucleus, the released protons begin to interact with the electrons,
which remain in the atom. As a result, binding energy of the electrons
remaining in the atom is increased. When one electron remains in the atom, it
interacts with all protons of the nucleus, and its binding energy with the
nucleus is increased proportionally to square of the number of the protons in
the nucleus.
It means that all electrons of the
atoms have approximately the same binding energies with the nucleus as the
electron of the hydrogen atom. Later on we’ll see that this assumption is
correct. Now let us calculate the spectra of two electrons of the oxygen atom.
The smallest ionization energy of
the electron of the oxygen atom is equal to ![]() =13.618 eV, and binding energy of this electron with the
atomic nucleus corresponding to the first energy level is equal to
=13.618 eV, and binding energy of this electron with the
atomic nucleus corresponding to the first energy level is equal to ![]() =13.752 eV. Let us call this electron the first one. The
calculation of energy indices of this electron according to the formulae (206)
and (207) give the following results (Table 21).
=13.752 eV. Let us call this electron the first one. The
calculation of energy indices of this electron according to the formulae (206)
and (207) give the following results (Table 21).
Table 21. Spectrum of the first
electron in the oxygen atom
|
Valumes |
n |
2 |
3 |
4 |
5 |
6 |
|
|
eV |
10.18 |
12.09 |
12.76 |
13.07 |
13.24 |
|
|
eV |
10.16 |
12.09 |
12.76 |
13.07 |
13.24 |
|
|
eV |
3.44 |
1.53 |
0.86 |
0.55 |
0.38 |
Ionization energy of the second
electron of oxygen atom is equal to ![]() =35.116 eV, and its binding energy with the atomic nucleus
corresponding to the first energy level
=35.116 eV, and its binding energy with the atomic nucleus
corresponding to the first energy level ![]() =83.98 eV. We’d like to draw the attention of the readers to
large divergences of experimental data concerning the second potential of
ionization, which are available in the reference books [5] and [25]. We trust
the new data being available in the reference book [5]. Taking into
consideration the above-mentioned facts the spectrum of the second electron of
oxygen atom has proved to be as follows (Table 22).
=83.98 eV. We’d like to draw the attention of the readers to
large divergences of experimental data concerning the second potential of
ionization, which are available in the reference books [5] and [25]. We trust
the new data being available in the reference book [5]. Taking into
consideration the above-mentioned facts the spectrum of the second electron of
oxygen atom has proved to be as follows (Table 22).
Table 22. Spectrum of the second
electron of the oxygen atom
|
Values |
n |
2 |
3 |
4 |
5 |
6 |
|
|
eV |
14.12 |
25.83 |
29.81 |
31.73 |
32.88 |
|
|
eV |
14.12 |
25.79 |
29.87 |
31.76 |
32.78 |
|
|
eV |
21.00 |
9.33 |
5.25 |
3.36 |
2.33 |
As it is known, chlorine is the 17th
element of the periodic law of chemical elements. Ionization potential of its
1st electron is ![]() =12.967 eV, and its binding energy with the atomic nucleus
corresponding to the first energy level is
=12.967 eV, and its binding energy with the atomic nucleus
corresponding to the first energy level is ![]() =15.548 eV. Experimental and theoretical values of energies
=15.548 eV. Experimental and theoretical values of energies ![]() of the photons being
absorbed and emitted by this electron corresponding to various energy levels
and binding energies
of the photons being
absorbed and emitted by this electron corresponding to various energy levels
and binding energies ![]() of this electron with
the nucleus of the chlorine atom are given in Table 23.
of this electron with
the nucleus of the chlorine atom are given in Table 23.
Table 23. Spectrum of the 1st
electron of the chlorine atom
|
Values |
n |
2 |
3 |
4 |
5 |
6 |
|
|
eV |
9.08 |
11.25 |
12.02 |
12.34 |
12.53 |
|
|
eV |
9.08 |
11.24 |
11.99 |
12.34 |
12.54 |
|
|
eV |
3.89 |
1.72 |
0.97 |
0.62 |
0.43 |
Copper is the 29th element of the
periodic law of chemical elements. Ionization potential of its 1st electron is ![]() =7.724 eV, and its binding energy corresponding to the first
energy level is
=7.724 eV, and its binding energy corresponding to the first
energy level is ![]() =98.85 eV. The rest energy indices of this electron are given
in Table 24.
=98.85 eV. The rest energy indices of this electron are given
in Table 24.
Table 24. Spectrum of the 1st electron of the copper atom
|
Values |
n |
5 |
6 |
7 |
8 |
9 |
|
|
eV |
3.77 |
4.97 |
5.72 |
6.19 |
6.55 |
|
|
eV |
3.77 |
4.98 |
5.71 |
6.18 |
6.50 |
|
|
eV |
3.96 |
2.75 |
2.02 |
1.54 |
1.22 |
Gallium is the 31st element.
Ionization potential of its 1st electron is ![]() =6.00 eV, and energy corresponding to the first energy level
is
=6.00 eV, and energy corresponding to the first energy level
is ![]() =46.88 eV. Other energy indices of this electron are given in
Table 25.
=46.88 eV. Other energy indices of this electron are given in
Table 25.
Table 25. Spectrum of the 31st
electron of the gallium atom
|
Valumes |
n |
4 |
5 |
6 |
7 |
8 |
|
|
eV |
4.11 |
4.71 |
5.06 |
5.23 |
5.40 |
|
|
eV |
4.12 |
4.70 |
5.04 |
5.27 |
5.42 |
|
|
eV |
2.93 |
1.87 |
1.30 |
0.96 |
0.73 |
The first electron of the sodium
atom (Na) has the smallest binding energies with the nucleus, that’s why it is the
main valency electron of this atom (Table 26). Ionization energy of the first
electron of the sodium atom is equal to ![]() =5.139 eV, and binding energy with the nucleus corresponding
to the first energy level is
=5.139 eV, and binding energy with the nucleus corresponding
to the first energy level is ![]() =13.086 eV. If we insert these results into the formulas
(206) and (207), we’ll find (Table 26).
=13.086 eV. If we insert these results into the formulas
(206) and (207), we’ll find (Table 26).
Table 26. Spectrum of the 1st
electron of the sodium atom
|
Valumes |
n |
2 |
3 |
4 |
5 |
6 |
|
|
eV |
- |
3.68 |
4.31 |
4.62 |
4.78 |
|
|
eV |
- |
3.68 |
4.32 |
4.62 |
4.77 |
|
|
eV |
3.27 |
1.45 |
0.82 |
0.52 |
0.36 |
In Table 26 theoretical ![]() (theor.) and
experimental
(theor.) and
experimental ![]() (exper.) values of
energies of the photons emitted and absorbed by this electron are given as well
as its binding energies
(exper.) values of
energies of the photons emitted and absorbed by this electron are given as well
as its binding energies ![]() (theor.) with the
atomic nucleus calculated according to the formulas (206) and (207). We’d like
to draw your attention to the fact that the second energy level of this electron
is fictitious (as the first one).
(theor.) with the
atomic nucleus calculated according to the formulas (206) and (207). We’d like
to draw your attention to the fact that the second energy level of this electron
is fictitious (as the first one).
Modern theories of formation of
molecules establish only the value of energy being necessary, as they say, for
a transfer of one electron and estimate it as being equal to 1.2-1.3 eV. This
is binding energy of the electron with the nucleus of unknown energy level.
As it is clear from our analysis,
each electron has a series of binding energies. A new theory gives the
opportunity to calculate these energies for any energy level of the electron
and to determine the number of this level and, consequently, the distance
between the atomic nucleus and valency electron.
We’ll continue analysis of binding
energies of the electrons with the atomic nuclei during consideration the
structures of the atoms of chemical elements.
We finish the presentation of the
theory of formation of the spectra of the atoms and the ions, and we should
note important issues for those who are going to continue these investigations.
First of all, it is only the beginning. It is based on the results of
experiments. If the results of the experiment differ from the actual spectrum
of this or that electron, the search process of energy ![]() becomes very
complicated. As the value of this energy is based on the value of excitation
energy, which is the first one in the row of all excitation energies
corresponding to the stationary energy levels, the exact definition of the
first excitation energy plays a decisive role. But the existing reference books
concerning spectroscopy do not meet this requirement. For example, let us take
excitation energies corresponding to the stationary energy levels of the second
electron of the carbon atom.
becomes very
complicated. As the value of this energy is based on the value of excitation
energy, which is the first one in the row of all excitation energies
corresponding to the stationary energy levels, the exact definition of the
first excitation energy plays a decisive role. But the existing reference books
concerning spectroscopy do not meet this requirement. For example, let us take
excitation energies corresponding to the stationary energy levels of the second
electron of the carbon atom.
The reference book written by
Striganov [5] contains the following row of these energies: 5.33; 9.29; 11.96;
13.71; 13.72; 14.45; 18.04; 19.49; 20.84;
21.49; 22.13; 22.47; 22.57; 22.82; 23.38; 26.58 eV. In the
reference book written by Zaidel, this row has the following values: 9.30;
11.96; 13.72; 14.46; 16.32; 17.62; 18.04; 18.06;
18.66; 19.49; 20.14; 20.84; 20.91; 20.95; 22.13; 22.54; 22.56;
22.90; 23.11; 24.27; 24.37; 24.59; 24.64; 25.98; 27.41; 27.47; 27.48 eV.
The underlined values of energies
coincide in both reference books; the values, which are not underlined do not
coincide. As it is clear, it is not easy to find energy, which corresponds to
the first excitation level. It looks like that this task should be solved by
means of an increase of the number of reference books used during the analysis
and elaboration of a special computer program, which could provide the solution
of the problem being set. If there are such rows of energies, which do not obey
the law (207), it will mean that at the moment of absorption and emission of
the photon, spin of the given electron is not parallel to spin of the photon.
In other words: a cell of such electron occupies non-standard place in the
atom.
8.9. THE NEW INTERPRETATION OF PHOTOEFFECT
It is known that the most acceptable
interpretation of experimental dependencies of photoeffect has been suggested
by A. Einstein in 1905, and he got the Noble prise for it [24], [111], [122].
He made it in the absence of the law of formation of the atom and ion spectra.
Now this law has been discovered, and we can check correctness of its interpretation
and the possibility of deeper understanding of photoeffect.
The mathematical model suggested by A. Einstein
for the interpretation of experimental dependencies of photoeffect has the
following form [122]
![]() , (226)
, (226)
where ![]() is kinetic energy of
the photoelectron emitted by the photocathode;
is kinetic energy of
the photoelectron emitted by the photocathode; ![]() is energy of the
photon, but it is not explained in the papers, of which photon exactly,
is energy of the
photon, but it is not explained in the papers, of which photon exactly, ![]() is the photoelectron exit work is a constant, which does not
depend on frequency [111]. The main experimental dependencies of photeffect are
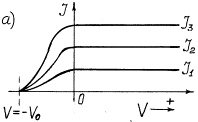
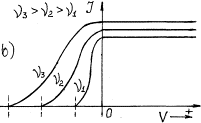
given in Fig. 20 [111].
is the photoelectron exit work is a constant, which does not
depend on frequency [111]. The main experimental dependencies of photeffect are
given in Fig. 20 [111].
Photocurrent takes place in the
photocathode-collector circuit. If the photocathode is exposed to monochromatic
light (Fig. 20, a), the value of
potential –![]() retarding the photoelectrons emitted by the photocathode
does not depend on light intensity. Light intensity increase increases
photocurrent and does not exert influence on the retarding potential value and,
consequently, on kinetic energy of the photoelectrons. If frequency of light,
which strikes upon the photocathode, is increased, the value of the negative
potential –
retarding the photoelectrons emitted by the photocathode
does not depend on light intensity. Light intensity increase increases
photocurrent and does not exert influence on the retarding potential value and,
consequently, on kinetic energy of the photoelectrons. If frequency of light,
which strikes upon the photocathode, is increased, the value of the negative
potential –![]() retarding the photoelectrons is increased (Fig. 20, b).
retarding the photoelectrons is increased (Fig. 20, b).
As the value of the retarding
negative potential –![]() is determined by kinetic energy
is determined by kinetic energy ![]() of the electrons
emitted by the photocathode under the influence of light illumination, it
results from the dependence shown in Fig. 20,b that kinetic energy
of the electrons
emitted by the photocathode under the influence of light illumination, it
results from the dependence shown in Fig. 20,b that kinetic energy ![]() of the photoelectrons
emitted by them is increased with the increase of frequency of the photons exposing
the photocathode.
of the photoelectrons
emitted by them is increased with the increase of frequency of the photons exposing
the photocathode.
Let us try to find a connection of Einstein’s equation (226) with the
mathematical model of the law of formation of the atom and ion spectra (207).
|
|
|
Fig. 20. Dependence of photocurrent
on light intensity: a) at its constant frequency; b) at different frequency ![]()
The correlation (207) appears from
experimental spectroscopy, that’s why it is a mathematical model of the law of
formation of the atom and ion spectra. Einstein’s equation (226) describes
similar process of photon absorption by the electrons. It affords ground for
supposition of identity of the
equations (207) and (226) and uniformity of their interpretation. It appears
from the given equations
![]() . (227)
. (227)
It means that if the electron loses
bond with the atomic nucleus, its kinetic energy ![]() is equal to energy
is equal to energy ![]() of the absorbed
photon. Then
of the absorbed
photon. Then
![]() . (228)
. (228)
It appears from this that ![]() energy value in
Einstein’s equation (226) is ionization energy
energy value in
Einstein’s equation (226) is ionization energy ![]() of the electron emitted
by the photocathode material. It appears from the equations (207) and (226)
that
of the electron emitted
by the photocathode material. It appears from the equations (207) and (226)
that
![]() .
(229)
.
(229)
The new clarification: photoelectron
exit work ![]() is equal to binding
energy of electron
is equal to binding
energy of electron ![]() when it is on a definite
energy level in the atom or the molecule.
when it is on a definite
energy level in the atom or the molecule.
Experimental investigations of photo
effect are carried out usually with the photocathodes made of alkali metals
[122]. For example, it is known that the work of the photoelectron exit from
the lithium photocathode is equal to ![]() =2.4 eV [122]. Ionization energy of this electron is equal to
=2.4 eV [122]. Ionization energy of this electron is equal to
![]() =5.392 eV, and its binding energy with the nucleus corresponding
to the first energy level is equal to
=5.392 eV, and its binding energy with the nucleus corresponding
to the first energy level is equal to ![]() =14.05 eV. If we take it into account and use the
mathematical model of the law of formation of the atom and ion spectra (207),
we’ll get a theoretical spectrum of this electron
=14.05 eV. If we take it into account and use the
mathematical model of the law of formation of the atom and ion spectra (207),
we’ll get a theoretical spectrum of this electron ![]() (theor.), which
coincides completely with the experimental spectrum
(theor.), which
coincides completely with the experimental spectrum ![]() (exp.) (Table 15). Formula (229) gives an opportunity to
calculate binding energies
(exp.) (Table 15). Formula (229) gives an opportunity to
calculate binding energies ![]() of this electron with
the atomic nucleus (according to
Einstein, the exit work), which correspond to all (
of this electron with
the atomic nucleus (according to
Einstein, the exit work), which correspond to all (![]() ) energy levels of this electron (Table 15).
) energy levels of this electron (Table 15).
It is known that the like atoms are
united in a molecule with the covalent bond, and binding energies between
valence electrons correspond to fractional quantum numbers ![]() . It allows us to determine what is a photoelectron emission
source: atoms or molecules of the photocathode material. If we substitute
. It allows us to determine what is a photoelectron emission
source: atoms or molecules of the photocathode material. If we substitute ![]() =2.4 eV and
=2.4 eV and ![]() =14.05 eV in the formula (229), we’ll find
=14.05 eV in the formula (229), we’ll find ![]() =2.4. As value
=2.4. As value ![]() is a fractional
number, it means that the lithium molecules, not atoms are the source of the
photoelectrons (Table 15).
is a fractional
number, it means that the lithium molecules, not atoms are the source of the
photoelectrons (Table 15).
For a photoelectron of the sodium
photocathode, we have: ![]() =5.139 eV,
=5.139 eV, ![]() =13.086 eV and
=13.086 eV and ![]() =2.1 eV [24.] If we use the mathematical model of the law of
formation of the atom and ion spectra (207), we’ll get a sodium photoelectron
spectrum (Table 26).
=2.1 eV [24.] If we use the mathematical model of the law of
formation of the atom and ion spectra (207), we’ll get a sodium photoelectron
spectrum (Table 26).
Value ![]() determined with the help of the formula (229) is equal to
determined with the help of the formula (229) is equal to ![]() =2.5. It appears from this that the sodium molecules,
not atoms are the source of the photoelectrons of the sodium photocathode.
=2.5. It appears from this that the sodium molecules,
not atoms are the source of the photoelectrons of the sodium photocathode.
The mathematical model of the law of formation of the atom and ion
spectra (207) shows that it has no orbital component of electron energy. It
appears from this that the electron has no orbital motion in the atom. The
molecules are formed by means of a combination of the unlike magnetic poles of
their valence atomic electrons, which are connected with the nuclear protons by
means of the magnetic poles as well.
The analysis of the law of formation
of the atom and ion spectra (207) as well as the spectrum calculation results
(Table 15 and 26) show that binding energy ![]() of the electron with
the atomic nucleus and, consequently, binding energy of valence electrons of
two atoms with each other is changed step by step (229). It appears from this
that kinetic energy of the photoelectrons
of the electron with
the atomic nucleus and, consequently, binding energy of valence electrons of
two atoms with each other is changed step by step (229). It appears from this
that kinetic energy of the photoelectrons ![]() and value of
retarding potential –
and value of
retarding potential –![]() (Fig. 20, b) should be changed step by step as well. The
photoelectrons can absorb only the photons, which correspond to their binding
energies in the molecules of the given substance. The greater binding energy
between the electrons in the molecules, the greater photon energy is required
for the break of this bond and the greater kinetic energy the photoelectrons
being released will acquire, and the greater potential will be required for
their retardation on the way to the collector. Let us pay attention to the fact
that the given logical chain originates from the mathematical model of the law
of formation of the atom and ion spectra (207) and is present in Einstein’s
equation implicitly (226).
(Fig. 20, b) should be changed step by step as well. The
photoelectrons can absorb only the photons, which correspond to their binding
energies in the molecules of the given substance. The greater binding energy
between the electrons in the molecules, the greater photon energy is required
for the break of this bond and the greater kinetic energy the photoelectrons
being released will acquire, and the greater potential will be required for
their retardation on the way to the collector. Let us pay attention to the fact
that the given logical chain originates from the mathematical model of the law
of formation of the atom and ion spectra (207) and is present in Einstein’s
equation implicitly (226).
Current is present in the circuit
due to the fact that the photoelectrons emitted by the photocathode material
molecules are substituted by free electrons. They should emit the photons, which
energy is equal to binding energy of the electrons in the molecules, but light
striking the photocathode does not allow us to see this emission.
Mathematical Einstein’s equation
(226) describing experimental regularities of photo effect has deeper physical
sense. When the components of this equation are interpreted correctly, it
becomes the mathematical model (207) of the law of formation of the atom and ion
spectra discovered by us in 1993 and published in the papers [18], [26], [33],
[53].
The
Foundations of Physchemistry of Microworld
Copyright Ó2003 Kanarev Ph.
M.
Internet Version - http://book.physchemistry.innoplaza.net
<< Back to Physchemistry Book Index