<<
Back to Kanarev's Physchemistry Book Index
6. MODEL OF ELECTRON AND PROTON
6.1. General Data on Electron
Let us pay attention to the fact
that the interaction between electromagnetic structures of the atom takes place
without resistance observation. If you ever held the magnets in your hands and
tried to bring their like poles nearer each other, you felt resistance and
complete lack of this resistance at the time when you displaced one magnet
relatively to another. In that case you felt their free relative displacement.
The same takes place when electromagnetic structures interact in the atom. It
cannot be otherwise. In all other cases the law of conservation of angular
momentum fails to operate.
In contrast to the photon, the
electron is at rest under the conditions
when it is in space and when no external force influences it. But it spends
greater part of its life in the atom. Here it works constantly supporting
equilibrium between energy state of the atom and energy state of the
environment. If surplus of some or other photons is available in the environment,
it begins to absorb them immediately in order to support disturbed equilibrium.
If there is a lack of some photons in the environment, the electron of the atom
begins to radiate these photons intensively in order to support a new energy
level of the environment. This process takes place in the Universe constantly;
it is not stopped even for a second.
If the electron did not function in
such a way, we’d never get warm in case we were cold. We can see the importance
of the function performed by electrons! If you get warm, please, note that it
is warmth from the electrons of your body, which have absorbed the photons from
the environment. If you are cold, please, note that the electrons have deprived
you of the photons and have radiated them into the environment. That’s why you
dress warm when the weather is cold. You do it in order to reduce radiation of
the photons.
It is very important to understand
that after the electron has absorbed the photon, the electron moves away from
the atomic nucleus. This is the main cause of expansion of gases and bodies
when they are heated. After photon radiation it gets nearer to the atomic
nucleus. This is the main cause of reduction of volumes of gases and sizes of
solids during their cooling. Using this general information let us begin to
find an electromagnetic model of the electron. For this
purpose, let us analyse the existing notions concerning its orbital motion
round the atomic nucleus.
6.2. Orbital Motion of the Electron
in the Atom
It is supposed that when the
electron moves in its orbit, it is influenced by two forces: Coulomb’s force 
, which attracts it
to the nucleus, and the centrifugal force of inertia 
, which withdraws it from the atom. It is considered that the
electron 
being the material
point is kept on a definite orbit due to equality between the above-mentioned
forces (Fig. 12).
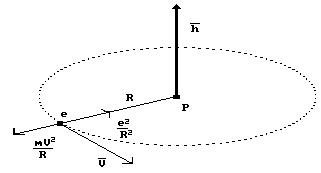
Fig. 12. Diagram of planetary motion
of the point model of the electron
(132)
It is not difficult to see that equality
between potential 
and kinetic 
energies of the electron
originates from equality of these forces.
.
(133)
Orbital velocity 
of the electron
depends on angular frequency 
of its orbital
rotation and radius 
of the orbit (Fig.
12)
.
(134)
Then the formula (133) will be written in such
a way
, (135)
where: 
is Planck’s constant.
. (136)
As the equation (135) describes the
bond between potential and kinetic energies of the electron in the hydrogen
atom, it should correspond to the data of experimental spectroscopy. According
to these data, when the electron passes from the first orbit to the second one,
its binding energy with the nucleus is reduced from 13.6 eV to 3.4 eV, i.e.
fourfold. The right part of the equation (135) shows that this reduction takes
place due to the reduction of angular frequency 
of rotation of the
electron, because 
. The preservation of equality between the right and the left
parts of the equation (135) is possible if orbital frequency 
is reduced fourfold,
radius 
of the orbit is
increased by the same magnitude.
Let us consider the expression of
orbital angular momentum of the electron (136). As centrifugal force of inertia
and Coulomb force of attraction of the electron to the nucleus are directed
radially (Fig. 12), they change only its mechanical trajectory and cannot
change rotation rate of the electron. That’s why in this case the law of
conservation of angular momentum should operate (136). It is manifested in the
following way.
When the electron passes from the
first orbit to the second one, it absorbs the photon with the mass, which is
almost 1000fold less than the mass of the electron itself. It means that the
conservation of persistence of Planck’s constant in the expression (136) takes
place mainly at the expense of the change of the values 
and 
. But during the analysis of the formula (135) we have
already shown that it appears from the experimental spectroscopy that the value
is reduced fourfold
when the electron passes from the first orbit to the second orbit, and radius
of the orbit R is increased by the same magnitude. It is clear that if 
is reduced fourfold
in the expression of Planck’s constant (136), value 
should be increased fourfold as well in order
to preserve this equality, but it is reduced sixteenfold, and it leads to the
violation of persistence of Planck’s constant, i.e. to the violation of the law
of conservation of orbital angular momentum (136). Such result points to the
fact that the electron of the hydrogen atom has no orbital motion. Later on
when we analyse the spectrum of the hydrogen atom, we’ll get additional proof
of the absence of orbital motion of the electron in the atom.
Thus, if we take a material point as a model of
the electron, the data of experimental spectroscopy show that such electron has
no orbital motion.
6.3. The model of electron is as a ring
It is known that the electron has
its own energy which is usually determined according to the formula 
. But the meaning of such an assumption is deciphered not
always. And the meaning is that if the
whole energy of the electron is transformed into energy of the photon, its energy becomes equal to 
. This fact has a strong experimental confirmation. It is
known the masses of electron and positron are equal. When they interact they
form two 
– photons. That’s why the energy of the photon which has the
corresponding mass can be attributed to the electron. Electron rest mass 
is determined with
great accuracy. Let us call electron energy 
being equal to photon
energy a photon energy of electron.
First of all, let us investigate the
possibilities of the ring model of free electron. It is known that the electron
has kinetic energy and potential energy which are equal to each other [168],
[176].
(137)
The calculation according to this
formula gives the following value of photon energy of the electron:
(138)
If free electron rotates only
relatively to its axis, angular frequency 
of rotation of ring
model of free electron determined according to the formula (137) is equal to
(139)
and radius of the ring is equal to
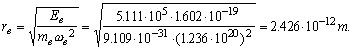(140)
Velocity of 
points of the
rotating ring is equal to velocity of light:
(141)
Let us try to memorize the obtained
values 
and 
. We shall get the same values, but with the help of other
formulas, which contain electromagnetic characteristics of the electron.
We should pay attention to the
following fact here. In classical mechanics the simplified models are often used
instead of the actual objects. The same has taken place in this case as well.
We have not found out the structure of the electron, but we have obtained its
simplified model – the ring. This model helps us to analyze mechanical behavior
of the electron, but it contains no information concerning its electromagnetic
properties. Let us try to find such mathematical models which describe behavior
of the ring model of the electron, which contain its charge 
, magnetic moment 
and electron
electromagnetic field strength 
(magnetic induction
of electron).
If we assume that the electron
charge is distributed uniformly along the length of its ring model, each
element of the ring 
will have mass 
and charge 
(Fig. 13). In this
case the rotating ring model of the electron will resemble ring current, and
two forces which have equal values and opposite directions: inertial force 
and Lorentz force 
(Fig. 12).
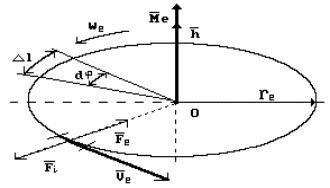
Fig. 13. Diagram of ring model of
the electron
(142)
Let us pay attention to the fact
that there are two notions for the magnetic field characteristic which are
similar as far as physical sense is concerned: magnetic field induction 
and magnetic field
strength 
which are connected
by the dependence
where 
is magnetic constant.
The analysis experience shows that
it creates a certain confusion during the formation of the ideas concerning
magnetic field, that’s why some authors refuse to use a clumsy term “magnetic
induction” and preserve only one, more felicitous term “magnetic field
strength” using symbol 
for it. Cl. E.
Suortz, the author of the book “Unusual physics of usual phenomena” [34], acted
in this way, and we follow his example. Magnetic field will be characterized by
vector 
, it will be called magnetic field strength measured in SI
system in T (Tesla) [177].
Then the dimensions of left and
right parts of formulae (142) will be:
If we write 
for mass density of
the ring and 
for charge density, we shall have
(143)
(144)
As:
(145)
(146)
and 
, the equation (142) assumes the form
(147)
or
(148)
Thus, we have got the mathematical
relation which includes: mass 
of free electron, its
charge 
, magnetic field strength 
inside the electron
ring which is generated by rotating ring charge, angular frequency 
and radius 
of the electron ring.
Magnetic moment of electron or, as it is called, Bohr magneton is missing in
this relation which mathematical presentation is as follows
(149)
Let us pay attention to the fact
that in the above-mentioned relation 
is vector value; it
gives vector properties to Bohr magneton 
as well. It follows
from the formula (149) that the directions of vectors 
and 
coincide. Let us convert the relation (148) in the following
way
(150)
The result from it is as follows
(151)
The left part of this relation can
be considered as scalar product of two
vectors: 
and 
. Energy value 
is vector as well. We
have come across vector properties of
single electron energy. Let us recollect that when we have considered the
processes of radiation and absorption of the photons by the electrons we have
found out that their energies are equal to vector products of two parallel
vectors 
and 
. Mathematical
model of energy of the electron has the same dependence (151).
Now from the relations (151) we can
determine magnetic field strength 
inside the ring mode
of the electron, angular velocity 
, rotations of the ring and its radius 
(152)
Let us pay attention to rather large
magnetic field strength in the centre of symmetry of the electron and let us
remind that it diminishes along the
electron rotation axis directly proportional to the square of a distance from
this centre [34]. We find from the relations (151)
(153)
As peripheral velocity of the ring
points is equal to velocity of light, we have
(154)
The main parameters of the ring
model of free electron: ring radius 
(140), (154) and
angular frequency of its rotation (139), (153) determined from the different
relations (137) and (150) have turned out to be equal.
A drawback of the ring model is in
the fact that it does not open a cause of positron birth, that’s why the
intuition prompts that the ring should have some internal structure. Our next
task is to find out this structure.
Before we begin to solve this task,
let us pay attention to the diagram of the ring model of the electron which
results from our calculations (Fig. 13). A coincidence of the directions of
vectors 
is the main
peculiarity. The model of electron proves vector properties of Planck’s
constant 
and Bohr magneton 
. We see that these vectors play a decisive role in the
formation of atoms, iones and molecules.
We’d like to draw the attention of
the reader to the fact that in all cases of our electron behaviour analysis
Planck’s constant in the integer form plays the role of its spin. In modern
physics it is accepted to think that the photon spin is equal to 
, and the electron spin is equal to 0.5
. But the electron spin value (0.5
) is used only for the analysis of qualitative
characteristics of electron behaviour [24], [111], [122]. Value 
is used for
quantitative calculations. In our investigations the integer of angular
momentum 
is the spin of the
photon and the electron. It is used for quantitative calculations and
qualitative characteristics of
behaviour of both photon and electron.
6.4. Toroidal model of the
electron
Torus is the nearest “relative” of
the ring. For the beginning let us assume that torus is hollow. Let us
write for torus section circle radius
(Fig. 14). The area of its surface is determined according to the formula
(155)
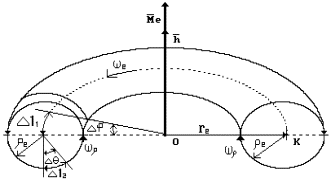
Fig. 14. Diagram of toroidal model
of the electron
Let us write 
for surface density
of electromagnetic substance of the
electron. Then
(156)
Let us determine moment of inertia
of hollow torus. We shall have the following equation from Fig. 14
(157)
(158)
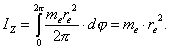(159)
As the electron demonstrates the
electrical properties and the magnetic ones at the same time and has angular
momentum, we have every reason to suppose that it has two rotations. Let us
call the usual rotation relative to the axis of symmetry with angular frequency
kinetic rotation
which forms its kinetic moment and kinetic energy. And secondly, let us call
vortical rotation relative to the ring axis with angular frequency 
(Fig. 14)
potential rotation which forms its potential energy and potential
properties. It is natural to assume that the sum of kinetic energy 
and potential energy 
of free electron is
equal to its photon energy 
. Let us consider the possibility of realization of our
suppositions. Kinetic energy of hollow torus rotation is determined according
to the formula (Fig. 14)
(160)
Frequency 
of kinetic rotation
of torus is equal to
(161)
We shall determine radius 
of torus from the formula (160)
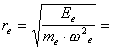
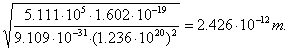(162)
As it is clear, 
and 
(162), (161) coincide
with the values of 
and 
in formulas (140),
(154), (139) and (153) in this case as well. It is interesting to find out if
there is an experimental confirmation of value 
obtained by us. It
turns out that there is such confirmation. In 1922 A. Compton, the American
physicist - experimenter, found that
dissipated X-rays had larger wave-length that incidental ones. He calculated
the shift of wave 
according to the
formula [3], [17], [24]
(163)
The experimental value of magnitude 
turned out to be equal
to 
[24]. Later on a
theoretical value of this magnitude was obtained by means of complex
mathematical conversions based on the ideas of
relativity 
.
When we have studied Compton effect
and have carried out its theoretical analysis, we have shown that the formula
for the calculation of theoretical value of Compton wave-length 
is obtained quite
simple if we attach sense of the electron radius to the electron wave-length
and consider the diagram of interaction of the ring model of electron with the
ring model of roentgen photon [17], [24], [97].
The diagram of interaction of the
ring model of roentgen photon with the ring model of the atomic electron is shown in Fig. 15.
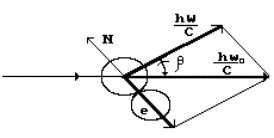
Fig. 15. Diagram of interaction of
the photon with the electron in Compton
effect
The pulse 
of the photon
falling on the electron and the pulse 
of the photon
reflected from the electron are connected by simple dependence
(164)
After the interaction of the photon with the
electron its pulse will be changed by the value
(165)
or
(166)
As
и
,
so
(167)
or
(168)
The relation can be converted in the following
way
(169)
As 
и
, the equation is as follows
(170)
This is Compton formula of the
calculation of the change of wave-length
of reflected roentgen
photon. Value 
being a constant is
called Compton wave-length. In the formula (170) it is a coefficient determined
experimentally and having the value [24,], [130]
(171)
which coincides completely with the
value of radius 
of the electron which has been calculated by us
theoretically according to the formula (140), (154) and (162)
(172)
It should be noted that we have obtained the formula (170) without
any relativity idea using only the classical notions concerning the interaction
of the ring models of the photon and the electron.
Thus, the value of 
of the ring
model of the electron obtained by us in
the calculation with the help of several methods when a various set of
characteristics of the electron has been used (140), (154) and (162) coincides
completely with the experimental value of Compton wave-length of the electron
(171).
As the analysis of the results of
experimental spectroscopy has shown that electron wave-length is equal to
radius of its ring model and as the results of various methods of the
calculation of radius of electron coincide completely with Compton experimental
result, the ring model of the electron is now the fact that is enough for the
resolute advancement in our search.
It is desirable to know the value of
radius 
of torus cross section circumference. Let us
try to find this value from the analysis of potential rotation of electron with
frequency 
(Fig. 14).
We should pay attention to the fact
that the pulse of both the photon and the electron is determined according to
one and the same relation
(173)
It means that both the photon and
the electron display their pulse in the interval of one wave-length. This fact
has been reflected in the models of the photon as an equality between
wave-length 
of the photon and its
radius 
. As the photon is absorbed and radiated by the electron, the
electron should have the same connection between the wave-length and radius.
Besides, the models of the photon has six electromagnetic fields; the same
quantity should be in the model of the electron when it radiates or absorbs the
photon. The described conditions prove to be fulfilled if one assumes that
angular frequency 
of kinetic rotation
is one-sixth of angular frequency 
of
potential rotation of free electron, i.e.
(174)
If we assume that velocity of the points of the
axis ring of torus in kinetic rotation is equal to velocity of the points of
the surface of torus in potential rotation, we shall have
(175)
From these relations we shall find out
(176)
and
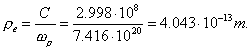(177)
If we substitute the data being
obtained into the formula (160), we shall find out the value of potential
energy 
of the electron
(178)
If we double this result, we shall obtain complete photon energy of free
electron (138). Complete coincidence of photon energy of the electron obtained
in different ways gives us the reason to suppose that the electron is a closed
ring vortex which forms a toroidal structure which rotates relatively its axis
of symmetry generating potential and kinetic energy.
It results from sixfold difference
between angular velocities 
and 
that radius 
is greater by sixfold
than radius 
. We postulate this fact supposing that, as we have shown,
the most economical mode of the photon movement is possible only at six
electromagnetic fields. This principle is realized when the vortex moves in a
closed helix of the torus. It results from the difference of radii and angular
velocity that the vortex which moves along the surface of torus makes six
rotations relative to the ring axis in a helix during one rotation of torus
relatively its axis of rotation. A lead of a helix is equal to radius 
of the axis ring and
wave-length 
of the electron (Fig.
16) [11], [15], [20], [29].
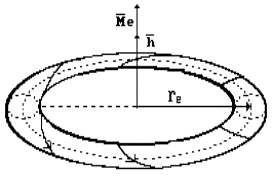
Fig. 16. Electron model diagram
Imagine now that external forces
begin to rotate such torus opposite to helix motion. Six vorticity, radial
directed fields are formed on the equatorial surface at once. External parts of
these six vortexes are outside the toroidal surface. As their peripheral
velocity is greater than velocity of light, this part is interrupted, and
lagging behind the rotational movement of torus it forms six chord-arranged
vorticity fields with unlike poles on their ends. They unite and form a
hexagon; as they move, six magnetic vorticity fields connected with each other
are formed. As the set of electrical field and magnetic field can exist only in
motion, such structure of the fields begins to move in space as an electromagnetic
formation which we call the photon.
The rest part of the electron
restores its vorticity and ring movement again having changed angular
velocities 
, 
and radii 
, 
, respectively, in
such a way that sixfold difference between them is preserved. Photon energy 
will be reduced,
respectively.
As energy of the electron is equal to Planck’s constant product by
angular frequency, energy of the electron will be reduced due to the reduction
of its angular frequency 
after photon
radiation. In order that Planck’s constant can preserve its permanency,
electron radius 
should be increased.
After the photon is absorbed, all its parameters are changed in the reverse
order.
We can imagine the details of the
processes of absorption and radiation of the photons by the electron and are
ready to begin to analyse them, but the lack of time makes us settle other
matters: to solve more important problems of the formation of the atoms, the
molecules, and, possibly, the atomic nuclei.
Let us compare binding energy of
hydrogen atom electron when it is on the first energy level (13.6 eV) with the
full (photon) energy of free electron 
eV. It becomes clear at once that an insignificant reduction
of energy (13.6 eV) of free electron will lead to almost inconspicuous increase
of radius 
when the bond is
formed between it and the proton. This radius will remain almost unchangeable
during the process of the transition.
Let us pay attention to one more
fact. Ionization energy of hydrogen-type atoms is equal to the product of
ionization energy of the hydrogen atom multiplied by the square of the number
of the element in the periodic table. For example, ionization energy of the
46th electron of the 46th element (palladium) is as follows
(179)
Ionization energy of the 100th
element (fermium) is as follows
(180)
Thus, when the palladium atom is
formed in the moment when its nucleus has no electrons, the free electron
forming a connection with such a nucleus radiates a photon or a series of
photons with the total energy of
28777.6 eV. Later on when it has an opportunity to absorb the photons,
this absorption will take place in such
a way that when the total energy of all absorbed photons becomes equal to
energy 28777.6 eV, energy of its bond with the nucleus becomes equal to zero,
and the full store of free electron energy will be restored.
Here it is appropriate to note an
interesting peculiarity. Full energy of the electron is equal to 
eV. When the 100th
element is formed, the electron uses 136000 eV of its full energy in order to
establish the connection with its nucleus. The question arises at once: which
is the maximal ordinal number N of the chemical element for the formation of
which full energy of the electron is enough? The following dependence gives the
answer to this question:
(181)
Certainly, it is unattainable limit.
In this case full energy of the electron will be spent for the bond with the
nucleus. Probably, there is a limit minimal value of energy of the electron
when it cannot be reduced anymore.
Free electron has potential
(vortical) rotation relative its ring axis and kinetic rotation relative to the
axis of symmetry. It radiates in the case when the external influence changes
the balance between these rotations.
Besides the translational motion and
rotary motion, in this case the electron has potential (vortical) rotation. We
have noted that a sharp change of the relations between kinetic and potential
rotations of the electron leads either to absorption or radiation of the photon
depending on the direction of the change of this relation. If this change slows
down kinetic rotation, the photon radiation process takes place; if this change
accelerates it, the absorption process takes place.
Modern relativists cannot withstand a flow of critic concerning their
erroneous notions. Trying to defend them they give the results of some
experiments, which, as they think, can be understood only on the grounds of
relativistic ideas. They include an experimental fact of the increase of mass
of the electron during the increase of velocity of its translational motion.
They interpret the result of this experiment with the help of relativistic
ratio
(182)
Actually, it follows from this ratio that with the increase of velocity 
of translational motion of the electron its mass m is
increased as compared with rest mass 
. Ask them: why and due to what does it take place? You will
get no answer, because their interpretation is based not on knowledge, but on
faith in correctness of Einstein’s ideas of relativity. They affirm that this
ratio can be obtained from the relativistic ideas only, not from other sources.
It appears from the Newton’s law that mass m of the body is connected
with force F influencing it and acceleration a with the dependence 
. It is clear from this dependence that mass can be increased
due to two factors: increase of force 
or reduction of
acceleration 
. But due to unknown reasons this opportunity is not used for
the analysis of this phenomenon and experimental check. One fails to measure
these values in the experiments with the electrons directly. That’s why one
tries to find indirect methods of explanation of this phenomenon.
In order to show that there can be several variants of development of
the formula (182) and the variants of its interpretation, we’ll try to find a
new development of this formula and a new interpretation connected with the
increase of rest mass of the electron during its accelerated motion. Motion of
the model of the electron in the electric field is shown in Fig. 17. As the
charge of the electron is formed on its toroidal surface, the direction of
motion of the electron in the electric field will be formed, first of all, by
the equatorial points of this surface. Both in free state and in motion the
electron has moment of momentum (angular momentum) 
, its
vector being directed along the axis of rotation of the torus [70].
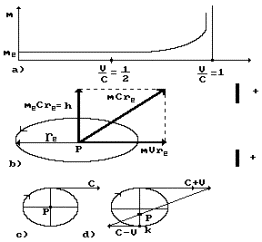
Fig. 17. Diagram of motion of the electron in
the electric field
Taking into consideration the fact that the accelerated motion of the
electron takes place under the predominance of the external influence, which
changes the state of the medium (in which the electron moves) forming certain
resistance to its motion, let us designate mass of the electron in its
translational motion via 
. It will mean that we have included coefficient of resistance
of medium, which is unknown to us, in symbol 
; hereby it differs from symbol 
in the expression of
moment of momentum. In this case, the pulse of the electron will be written in
the following way 
.
Thus, during the forced translational motion two vectors 
and 
, which are perpendicular to each other, are applied to the
electron (if we do not take into consideration the direction of the magnetic
field vector). The first one characterizes the rotation of the electron in relation
to its axis of symmetry; the second one characterizes translational motion. A
question arises: what total motion will the electron have in this case? It should
be characterized by vector value, which is equal to the sum of the first two
vectors. But we cannot add these vectors, because their numerical values have
different dimensionalities. In order to do away with this drawback, it is
necessary to change the numerical value of the second vector 
in such a way that
the dimensionalities of both vectors should be equal. For this purpose let us
multiply it by value 
. It is natural that the sum of the first two vectors will be
equal to the third vector, which should characterize two above-mentioned
motions of the toroidal model of the electron immediately (Fig. 17). In order
the third vector takes into account medium resistance as the second one, let us
designate mass of the electron with symbol 
in its expression.
Besides, the third vector should have the same dimensionality as the first two.
For this purpose let us multiply its numerical value by 
.
After such preparation we have the
right to find the geometrical sum of the first two vectors. From Fig. 17 we’ll
get
(183)
or
Finally,
we’ll determine
(184)
This is a famous relativistic ratio, which shows the
increase of mass of the electron when velocity of its translational motion is increased in the electric field. We
should note that main thing. We have got this ratio not in the pseudo-Euclidean
geometry by Minkovsky, but in Euclidean geometry and within the framework of
the space-matter-time unity axiom.
Now the kinematic sense of the ration 
is clear. When the
electron is influenced by none of the external forces, it rotates only in
relation to its axis, and in this case the instantaneous centre of rotation 
coincides with the
geometrical centre of the electron (Fig. 17 b, c).
As the electron receives translational notion, its instantaneous centre
of rotation P begins to withdraw from the geometrical centre to the periphery
of its toroidal structure (Fig. 17, d). When forward velocity 
gets nearer to
velocity 
, with which the ring axis of the torus rotates, the instantaneous
centre will withdraw from the geometrical centre of the electron by value 
(Fig. 17, d). All these
changes take place in the reference system connected with the observer or the
external source, which forms its accelerated translational motion forcibly.
Let us recollect that in this case, except translational and rotational
motions, the electron has potential (vortex) rotation. We have already noted
that a sharp change of the relations between kinetic and potential rotations of
the electron leads either to absorption or to emission of the photon depending
on the direction of the change of this relation. If this change slows down
kinetic rotation, the process of emission of the photon takes place; it the
change accelerates it, the process of absorption takes place.
It is easy to imagine that these both cases are possible during the alternating
motion of the electron in the electric field. In one of the cases emission of
the photons should be observed, it is called deceleration emission; in another
case absorption takes place, but not of the photons, but a substance of the medium formed by the electromagnetic
field, in which the electron moves. Roughly speaking, toroid of the electron
will wind lines of force of the field on itself and due to this fact it will
increase its mass at 
(Fig. 17, a).
Thus, we have every reason to suppose that energy and consequently mass
of the electron will be increased at the expense of absorption of the material
base of the medium, which increases its motion. We can call this medium the
ether. Even a cursory analysis of motion of the toroidal model of the electron
in the electric field gives the answers to the questions: why and at what
expense is the mass of the electron increased? These answers have all the
features, which give the opportunity to consider them as hypothetical ones at
the first stage. This is a way to the
truth, not to the faith.
A question arises: what development of the relation (182) and what variant
of its interpretation is nearer to the truth, the relativistic one or the one
considered by us?
Let us recollect that in this case, except translational and rotational
motions, the electron has potential (vortex) rotation. We have already noted
that a sharp change of the relations between kinetic and potential rotations of
the electron leads either to absorption or to emission of the photon depending
on the direction of the change of this relation. If this change slows down
kinetic rotation, the process of emission of the photon takes place; it the
change accelerates it, the process of absorption takes place.
When we have substantiated the model of the electron, we have used the
existing Coulomb’s law and Newton’s law, spectrum formation law formulated by
us, Lorentz electromagnetic force and the following constants: velocity of
light 
, Planck’s constant 
, electron rest mass 
, its charge 
, electron rest energy, Bohr magneton 
, electrical constant 
, Compton wavelength of the electron, which should be called
Compton radius of the electron and the ionization of the hydrogen atom.
Thus, the electron has the from of the rotating hollow torus (Fig. 16).
Its structure proves to be stable due to availability of two rotations. The
first rotation takes place about an axis, which goes through the geometrical
centre of torus perpendicular to the plane of rotation. The second rotation is
a vortical one about the ring axis, which goes through the torus cross section
circumference centre.
Several methods of torus radius
calculation which include its various energy and electromagnetic properties
give the same result which completely coincides with the experimental value of
Compton wave-length of the electron, i.e. 
[17], [70], [97].
Electron spin is its another
important characteristic. It is equal to Planck’s constant and is vector
quantity 
. Its vector
properties originate from the main dimensionality 
– moment of momentum
or angular momentum.
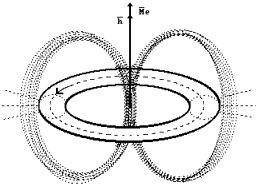
Fig. 18. Diagram of electromagnetic model of the electron
(only a part of electric and
magnetic lines of force is given in the figure)
The third important characteristic
of the electron – magnetic moment or Bohr magneton which generates strength 
of magnetic
field of the electron (Fig. 18). In its geometrical centre it is equal to 
. It is a significant value, but it is reduced with the increase
of the distance from the geometrical centre of the electron along the axis of
rotation according to dependence 
. Here 
is the distance from
the geometrical centre of the electron along its axis of rotation [34].
Only a part of magnetic lines of
force and the lines which characterize electric field of the electron is shown
in Fig. 18. If the whole set of these lines is shown, the model of the electron
will assume the form which resembles of the form of an apple. As the lines of
force of the electric field are perpendicular to the lines of force of the
magnetic field, the electric field in this model will become almost spherical,
and the form of the magnetic field will
resemble the magnetic field of a bar
magnet.
The
Foundations of Physchemistry of Microworld
Copyright Ó2003 Kanarev Ph.
M.
Internet Version - http://book.physchemistry.innoplaza.net
<< Back to Physchemistry Book Index